题目内容
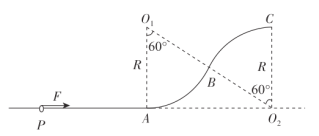
【题目】如图所示，半径均为
的光滑圆弧轨道
与
在
点平滑连接，固定在竖直面内，
端与固定水平直杆平滑连接，两段圆弧所对的圆心角均为60°，一个质量为
的圆环套在直杆上，静止在
点，
间的距离为
，圆环与水平直杆间的动摩擦因数
，现给圆环施加一个水平向右的恒定拉力
，使圆环向右运动，圆环运动到点时撤去拉力，结果圆环到达
点时与圆弧轨道间的作用力恰好为零，重力加速度
，求：
(1)拉力的大小；
(2)若不给圆环施加拉力，而是在点给圆环一个初速度
，结果圆环从点滑出后，下落高度时的位置离
点距离也为
，初速度应是多大。
【答案】(1)
；(2)
【解析】
(1)圆环到
点时对轨道的压力恰好为零，设到点的速度大小为
，则
可得
根据动能定理
求得拉力的大小
(2)圆环从点抛出后，下落
高度时的位置离点水平距离为，设在点的速度为
，则
求得
从
到根据动能定理有
求得
练习册系列答案
暑假作业海燕出版社系列答案
相关题目
