题目内容
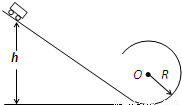
如图所示,光滑斜面末端与一个半径为R的光滑圆轨道平滑连接,一质量为m的小车(大小可忽略)小车从斜面上的某一高度由静止滑下,小车沿圆环轨道运动恰能越过圆弧轨道最高点.已知重力加速度为g.求:(1)小车在圆轨道最低点时的速度.
(2)小车下滑的高度h.
【答案】分析:(1)小球恰好能通过圆弧轨道最高点,说明此时恰好是物体的重力作为向心力,由向心力的公式可以求得在最高点的速度大小,由物体的机械能守恒求解最低点时的速度
(2)从开始到最低点由机械能守恒定律求解高度.
解答:解:(1)小车恰能越过圆轨道的最高点,它越过圆轨道的最高点的速度为v,由牛顿第二定律得:
mg=m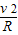 ,
,
解得:v=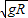
小车在最低点时的速度为v1,由机械能守恒定律得:
 mv2+2mgR=
mv2+2mgR= mv21
mv21
解得:v1=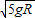
(2)设两车滑到圆轨道最低点时的速度为v,由机械能守恒定律得:
 mv21=mgh
mv21=mgh
小车下滑时高度h= R
R
答:(1)小车在圆轨道最低点时的速度是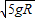 .
.
(2)小车下滑的高度是 R.
R.
点评:解决本题的关键熟练运用机械能守恒定律,以及知道在圆周运动的最高点和最低点,沿半径方向的合力提供向心力.
(2)从开始到最低点由机械能守恒定律求解高度.
解答:解:(1)小车恰能越过圆轨道的最高点,它越过圆轨道的最高点的速度为v,由牛顿第二定律得:
mg=m
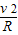 ,
,解得:v=
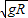
小车在最低点时的速度为v1,由机械能守恒定律得:
 mv2+2mgR=
mv2+2mgR= mv21
mv21解得:v1=
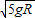
(2)设两车滑到圆轨道最低点时的速度为v,由机械能守恒定律得:
 mv21=mgh
mv21=mgh小车下滑时高度h=
 R
R答:(1)小车在圆轨道最低点时的速度是
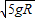 .
.(2)小车下滑的高度是
 R.
R.点评:解决本题的关键熟练运用机械能守恒定律,以及知道在圆周运动的最高点和最低点,沿半径方向的合力提供向心力.

练习册系列答案
相关题目
 如图所示,光滑斜面的倾角为θ,若将一小球在斜面上离底边长L处沿斜面水平方向以速度v0抛出,问小球滑到斜面底端时水平位移s是多大?末速度vt多大?
如图所示,光滑斜面的倾角为θ,若将一小球在斜面上离底边长L处沿斜面水平方向以速度v0抛出,问小球滑到斜面底端时水平位移s是多大?末速度vt多大?

 ,s=vt,
,s=vt, .
.
 ,s=vt,
,s=vt, .
.