题目内容
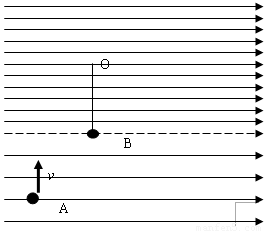
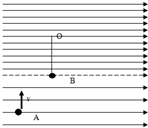 如图,虚线下方有足够大的场强大小E=5.0×103 V/m和上方场强为8mg/3q的匀强电场,方向均水平向右.质量均为m=1.5×10-2kg的A、B小球,其中B球为绝缘小球且不带电,被长为R的绝缘丝线悬挂在O点刚好静止在虚线上,A球带电荷量为qA=+6.0×10-6C,在竖直平面内的以某一初速度v竖直进入电场,运动到B点速度刚好水平,同时与B球发生正碰并立即粘在一起围绕O点做半径为R=0.7m完整的圆周运动,假设甲、乙两球可视为质点,g取10m/s2.(sin53°=0.8,c0s53°=0.6)
如图,虚线下方有足够大的场强大小E=5.0×103 V/m和上方场强为8mg/3q的匀强电场,方向均水平向右.质量均为m=1.5×10-2kg的A、B小球,其中B球为绝缘小球且不带电,被长为R的绝缘丝线悬挂在O点刚好静止在虚线上,A球带电荷量为qA=+6.0×10-6C,在竖直平面内的以某一初速度v竖直进入电场,运动到B点速度刚好水平,同时与B球发生正碰并立即粘在一起围绕O点做半径为R=0.7m完整的圆周运动,假设甲、乙两球可视为质点,g取10m/s2.(sin53°=0.8,c0s53°=0.6)(1)假设初速度v=20m/s,试求小球A与B球碰撞前能运动的水平位移的大小和整个过程中电场力对小球做功的最大值.
(2)如果小球刚好能做完整的圆周运动,试求碰撞前A球的最小速度和绳子所受的最大拉力分别多大.
分析:(1)小球A在竖直方向只受重力,做匀减速直线运动,水平方向在电场力作用下做匀加速直线运动,两个方向时间相等,根据匀变速直线运动的基本公式即可求解水平位移,根据恒力做功公式即可求解整个过程中电场力对小球做功的最大值;
(2)小球刚好能做完整的圆周运动,在最高点绳子的拉力为零,重力和电场力的合力提供向心力,根据向心力公式求出此时的速度,从最高点到B点的过程中运用动能定理求得在B点的速度,根据动量守恒定律求得碰撞前A球的最小速度,在最低点根据向心力公式求解绳子所受的最大拉力.
(2)小球刚好能做完整的圆周运动,在最高点绳子的拉力为零,重力和电场力的合力提供向心力,根据向心力公式求出此时的速度,从最高点到B点的过程中运用动能定理求得在B点的速度,根据动量守恒定律求得碰撞前A球的最小速度,在最低点根据向心力公式求解绳子所受的最大拉力.
解答:解:(1)A在竖直方向做匀减速直线运动,加速度为g,则有:
t=
=
=2s
水平方向在电场力作用下做匀加速直线运动,则有:
x=
at2=
×
×4m=4m
当小球和B粘在一起做圆周运动,运动到与O等高时,电场力做功最大,则
W=Eqx+E′qR=5.0×103 V×6.0×10-6C×4+
×q×0.7=0.4J
(2)碰撞前A球的速度为v0,碰撞后共同速度为v1,等效最高点速度为v2,
根据动量守恒定律得:
mv0=2mv1
等效最高点合力F=5×
=m
根据动能定理得:F(R+0.6R)=△EK
解得:v0=14m/s,v1=7m/s
最低点的速度为v′
在最低点,根据向心力公式得:
N-
mg=2m
又动能定理F×0.4R=△EK
解得:N=20mg=3N
答:(1)假设初速度v=20m/s,小球A与B球碰撞前能运动的水平位移的大小为4m,整个过程中电场力对小球做功的最大值为0.4J.
(2)如果小球刚好能做完整的圆周运动,碰撞前A球的最小速度为14m/s,绳子所受的最大拉力为3N.
t=
| v |
| g |
| 20 |
| 10 |
水平方向在电场力作用下做匀加速直线运动,则有:
x=
| 1 |
| 2 |
| 1 |
| 2 |
| 5000×6×10-6 |
| 1.5×10-2 |
当小球和B粘在一起做圆周运动,运动到与O等高时,电场力做功最大,则
W=Eqx+E′qR=5.0×103 V×6.0×10-6C×4+
| 8mg |
| 3q |
(2)碰撞前A球的速度为v0,碰撞后共同速度为v1,等效最高点速度为v2,
根据动量守恒定律得:
mv0=2mv1
等效最高点合力F=5×
| 2mg |
| 3 |
| v22 |
| R |
根据动能定理得:F(R+0.6R)=△EK
解得:v0=14m/s,v1=7m/s
最低点的速度为v′
在最低点,根据向心力公式得:
N-
| 10 |
| 3 |
| v′2 |
| R |
又动能定理F×0.4R=△EK
解得:N=20mg=3N
答:(1)假设初速度v=20m/s,小球A与B球碰撞前能运动的水平位移的大小为4m,整个过程中电场力对小球做功的最大值为0.4J.
(2)如果小球刚好能做完整的圆周运动,碰撞前A球的最小速度为14m/s,绳子所受的最大拉力为3N.
点评:本题主要考查了动能定理、动量守恒定律、圆周运动向心力公式的应用,要求同学们能正确分析物体的运动情况,选择适当的公式求解,难度较大.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目