题目内容
有一半径为R的圆形水池，某人绕池边以大小为v的线速度奔跑，同时从距水面h高处水平抛出一小石子，为使石子恰好落在池中心，试求抛出的石子相对于抛出者的初速度v0．
【答案】
【解析】石子抛出后作竖直方向上的自由落体运动，则下落时间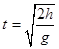
在t时间后，石子刚好落在池子中心，则水平方向的位移是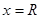
那么，水平方向的速度为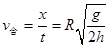
而水平方向的速度是随着人一起的切线方向上的速度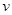
和人水平抛出石子的速度
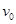的合速度
所以，由勾股定理可以得到：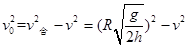
，所以
思路分析：水平方向的速度是随着人一起的切线方向上的速度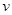和人水平抛出石子的速度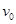的合速度，结合运动学规律解题
试题点评：本题与船过河的问题非常类似，利用运动的合成与分解知识解题，关键是知道水平方向的速度是随着人一起的切线方向上的速度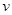和人水平抛出石子的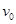速度的合速度，
练习册系列答案
相关题目
（2012?浙江模拟）如图甲所示，在圆形水池正上方，有一半径为r的圆形储水桶．水桶底部有多个水平小孔，小孔喷出的水在水池中的落点离水池中心的距离为R，水桶底部与水池水面之间的高度差是h．为了维持水桶水面的高度不变，用水泵通过细水管将洒落的水重新抽回到高度差为H的水桶上方．水泵由效率为η1的太阳能电池板供电，电池板与水平面之间的夹角为α，太阳光竖直向下照射（如图乙所示），太阳光垂直照射时单位时间、单位面积接受的能量为E0．水泵的效率为η2，水泵出水口单位时间流出水的质量为m0，流出水流的速度大小为v0（不计水在细水管和空气中运动时所受的阻力）．
