题目内容
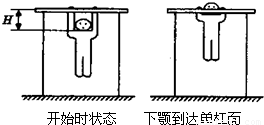
引体向上运动是同学们经常做的一项健身运动.如图所示,质量为m的某同学两手正握单杠,开始时,手臂完全伸直,身体呈自然悬垂状态,此时他的下颚距单杠面的高度为H,然后他用恒力F向上拉,下颚必须超过单杠面方可视为合格,已知H=0.6m,m=60kg,重力加速度g=10m/s2.不计空气阻力,不考虑因手弯曲而引起人的重心位置变化.(1)第一次上拉时,该同学持续用力(可视为恒力),经过t=1s时间,下颚到达单杠面,求该恒力F的大小及此时他的速度大小;
(2)第二次上拉时,用恒力F′=720N拉至某位置时,他不再用力,而是依靠惯性继续向上运动,为保证此次引体向上合格,恒力F的作用时间至少为多少.
【答案】分析:(1)第一次上拉时,该同学向上匀加速运动,写出牛顿第二定律方程和匀变速直线运动位移与时间的关系式联立求解;
(2)第二次上拉时,该同学先做匀加速度运动后做匀减速运动,末速度恰好等于零.位移和等于H,联立方程求解.
解答:解:(1)第一次上拉时,该同学向上匀加速运动,设他上升的加速度大小为a1,下颚到达单杠面时的速度大小为v,由牛顿第二定律及运动学规律可得:
F-mg=ma1
H= a1 t2
a1 t2
v=a1t
联立上式可得:F=672N
v=1.2m/s
(2)第二次上拉时,设上拉时的加速度大小为a2,恒力至少作用的时间为tmin,上升的位移为x1,速度为v1,自由上升时位移为x2,根据题意可得:
由牛顿第二定律得:F′-mg=ma2
由题意知:x1+x2=H
x1= a2tmin2
a2tmin2
v12=2gx2
v1=a2tmin
联立上式可得:tmin═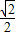 s=0.71s
s=0.71s
答(1)该恒力的大小为672N,他的速度1.2m/s
(2)该恒力最少的作用时间0.71s
点评:本题考查匀变速直线运动规律的应用和牛顿第二定律在解题中的作用.关键是找出第二次引体向上成功的临界条件即末速度等于零.是一道好题.
(2)第二次上拉时,该同学先做匀加速度运动后做匀减速运动,末速度恰好等于零.位移和等于H,联立方程求解.
解答:解:(1)第一次上拉时,该同学向上匀加速运动,设他上升的加速度大小为a1,下颚到达单杠面时的速度大小为v,由牛顿第二定律及运动学规律可得:
F-mg=ma1
H=
 a1 t2
a1 t2 v=a1t
联立上式可得:F=672N
v=1.2m/s
(2)第二次上拉时,设上拉时的加速度大小为a2,恒力至少作用的时间为tmin,上升的位移为x1,速度为v1,自由上升时位移为x2,根据题意可得:
由牛顿第二定律得:F′-mg=ma2
由题意知:x1+x2=H
x1=
 a2tmin2
a2tmin2 v12=2gx2
v1=a2tmin
联立上式可得:tmin═
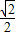 s=0.71s
s=0.71s 答(1)该恒力的大小为672N,他的速度1.2m/s
(2)该恒力最少的作用时间0.71s
点评:本题考查匀变速直线运动规律的应用和牛顿第二定律在解题中的作用.关键是找出第二次引体向上成功的临界条件即末速度等于零.是一道好题.

练习册系列答案
相关题目
 (2011?苏州一模)引体向上运动是同学们经常做的一项健身运动.如图所示,质量为m的某同学两手正握单杠,开始时,手臂完全伸直,身体呈自然悬垂状态,此时他的下颚距单杠面的高度为H,然后他用恒力F向上拉,下颚必须超过单杠面方可视为合格,已知H=0.6m,m=60kg,重力加速度g=10m/s2.不计空气阻力,不考虑因手弯曲而引起人的重心位置变化.
(2011?苏州一模)引体向上运动是同学们经常做的一项健身运动.如图所示,质量为m的某同学两手正握单杠,开始时,手臂完全伸直,身体呈自然悬垂状态,此时他的下颚距单杠面的高度为H,然后他用恒力F向上拉,下颚必须超过单杠面方可视为合格,已知H=0.6m,m=60kg,重力加速度g=10m/s2.不计空气阻力,不考虑因手弯曲而引起人的重心位置变化.

 的某同学两手正握单杠,开始时,手臂完全伸直,身体呈自然悬垂状态,此时他的下鄂距单杠面的高度为
的某同学两手正握单杠,开始时,手臂完全伸直,身体呈自然悬垂状态,此时他的下鄂距单杠面的高度为 ,然后他用恒力
,然后他用恒力 向上拉,下颚必须超过单杠面方可视为合格,已知
向上拉,下颚必须超过单杠面方可视为合格,已知 ,
, ,重力加速度
,重力加速度 .不计空气阻力,不考虑因手弯曲而引起人的重心位置变化.
.不计空气阻力,不考虑因手弯曲而引起人的重心位置变化.
 时间,下鄂到达单杠面,求该恒力
时间,下鄂到达单杠面,求该恒力 拉至某位置时,他不再用力,而是依靠惯性继续向上运动,为保证此次引体向上合格,恒力
拉至某位置时,他不再用力,而是依靠惯性继续向上运动,为保证此次引体向上合格,恒力 的作用时间至少为多少?
的作用时间至少为多少?