题目内容
质量为m=1kg的小木块（可看成质点），放在质量为M=5kg的长木板的左端，如图所示．长木板放在光滑的水平桌面上．小木块与长木板间的动摩擦因数μ=0.1，长木板的长度l=2m．系统处于静止状态．现使小木块从长木板右端脱离出来，可采取下列两种方法：（g取10m/s2）（1）给小木块施加水平向右的恒定外力F，F作用时间t=2s．则F至少是多大？
（2）给小木块一个水平向右的冲量I，则冲量I至少是多大？
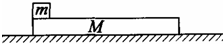
【答案】分析：（1）给小木块施加水平向右的恒定外力F，小木块向右做匀加速运动，长木板也向右做匀加速运动，撤去F后木块向右做功匀减速运动，木板继续向右做匀加速运动，当木块恰好滑到木板的右端时，木块与木板的位移之差等于板长，两者速度相等．根据动量定理、能量守恒定律和位移关系结合求解F的大小；
（2）给小木块一个水平向右的冲量I，使木块获得一个初速度，当木块恰好滑到木板的右端时，两者速度相等时，I最小．根据动量定理、系统的动量守恒和能量守恒求解I的最小值．
解答：解：（1）设F刚撤去时，木块与木板的速度分别为v1和v2，当木块恰好滑到木板的右端时，两者共同速度为v．
对于F作用过程，根据动量定理得：
对整体：Ft=mv1+Mv2 ①
对木板：μmgt=Mv2 ②
此过程木块在木板滑行的距离S1=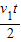
-
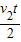③
对整体过程有，Ft=（m+m）v ④
对于撤去F到木块滑到木板右端的过程，设木块相对于木板滑行的距离为S2，根据能量守恒定律得
μmgS2=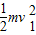
+
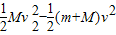⑤
又S1+S2=l，⑥
联立以上6式，解得，F=1.85N
（2）当木块恰好滑到木板的右端时，两者速度相等，I最小，则由系统动量守恒
mv=（m+M）v1
解得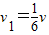
由能量守恒得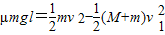
解得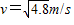
由动量定理得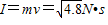
答：（1）给小木块施加水平向右的恒定外力F，F作用时间t=2s．F至少是2.2N；
（2）给小木块一个水平向右的冲量I，则冲量I至少是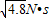
．
点评：第1题的解题关键是抓住木块与木板的位移关系；第2题关键是抓住隐含的临界状态：木块恰好滑到木板的右端时，两者速度相等，根据动量守恒和能量守恒结合求解．
（2）给小木块一个水平向右的冲量I，使木块获得一个初速度，当木块恰好滑到木板的右端时，两者速度相等时，I最小．根据动量定理、系统的动量守恒和能量守恒求解I的最小值．
解答：解：（1）设F刚撤去时，木块与木板的速度分别为v1和v2，当木块恰好滑到木板的右端时，两者共同速度为v．
对于F作用过程，根据动量定理得：
对整体：Ft=mv1+Mv2 ①
对木板：μmgt=Mv2 ②
此过程木块在木板滑行的距离S1=
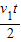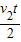- ③对整体过程有，Ft=（m+m）v ④
对于撤去F到木块滑到木板右端的过程，设木块相对于木板滑行的距离为S2，根据能量守恒定律得
μmgS2=
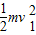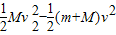+ ⑤又S1+S2=l，⑥
联立以上6式，解得，F=1.85N
（2）当木块恰好滑到木板的右端时，两者速度相等，I最小，则由系统动量守恒
mv=（m+M）v1
解得
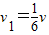
由能量守恒得
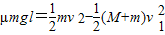
解得
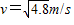
由动量定理得
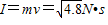
答：（1）给小木块施加水平向右的恒定外力F，F作用时间t=2s．F至少是2.2N；
（2）给小木块一个水平向右的冲量I，则冲量I至少是
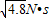．点评：第1题的解题关键是抓住木块与木板的位移关系；第2题关键是抓住隐含的临界状态：木块恰好滑到木板的右端时，两者速度相等，根据动量守恒和能量守恒结合求解．
练习册系列答案
相关题目
如图所示，光滑水平面上静止放着长L=1m，质量为M=3kg的木块，一个质量为m=1kg的小物体（可看作质点）放在木板的最右端，m和M之间的动摩擦因数μ=0.1，今对木板施加一水平向右的拉力F，（g取10m/s2）
如图所示，三角形木楔静置于粗糙水平地面上，木楔质量M=9kg、倾角θ=30°，三角形木楔的斜面上有一个质量为m=1kg的小物块．（重力加速度取g=10m/s2）
（2008?四川）如图，一质量为m=1kg的木板静止在光滑水平地面上．开始时，木板右端与墙相距L=0.08m；质量为m=1kg 的小物块以初速度v0=2m/s 滑上木板左端．木板长度可保证物块在运动过程中不与墙接触．物块与木板之间的动摩擦因数为μ=0.1．木板与墙的碰撞是完全弹性的．取g=10m/s2，求
如图所示，长为