题目内容
若取地球的第一宇宙速度为8km/s,某行星的密度与地球密度相近,半径是地球的
倍,则此行星的第一宇宙速度约为( )
| 1 |
| 2 |
分析:第一宇宙速度等于卫星绕行星附近做匀速圆周运动的速度,卫星的向心力由行星的万有引力提供,结合密度公式,列式求解.
解答:解:设行星的第一宇宙速度为v1,质量为M,半径为R,地球的第一宇宙速度为v1,地球质量为M0,半径为R0.卫星的质量为m.
则根据万有引力等于向心力,得:
G
=m
,
解得:v1=
;同理得,v2=
.
又M=ρ?
πR3,M0=ρ?
πR03.
联立上四式得:
=
=
,
得:v1=
v2=
×8km/s=4km/s
故选:B
则根据万有引力等于向心力,得:
G
| Mm |
| R2 |
| v2 |
| R |
解得:v1=
|
|
又M=ρ?
| 4 |
| 3 |
| 4 |
| 3 |
联立上四式得:
| v1 |
| v2 |
| R |
| R0 |
| 1 |
| 2 |
得:v1=
| 1 |
| 2 |
| 1 |
| 2 |
故选:B
点评:本题首先要理解并掌握第一宇宙速度的定义,其次掌握卫星问题常用的思路:万有引力等于向心力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目






 注入人体,
注入人体,
 D.液体表面层的分子比液体内部的分子有更大的分子势能
D.液体表面层的分子比液体内部的分子有更大的分子势能 D.超声波可以在真空中传播
D.超声波可以在真空中传播
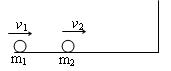
 ⑶如图所示,质量分别为m1和m2的两个小球在光滑水平面上分别以速度v1、v2同向运动,并发生对心碰撞,碰后m2被右侧墙壁原速弹回,又与m1碰撞,再一次碰撞后两球都静止.求第一次碰后m1球速度的大小.
⑶如图所示,质量分别为m1和m2的两个小球在光滑水平面上分别以速度v1、v2同向运动,并发生对心碰撞,碰后m2被右侧墙壁原速弹回,又与m1碰撞,再一次碰撞后两球都静止.求第一次碰后m1球速度的大小. D.液体表面层的分子比液体内部的分子有更大的分子势能
D.液体表面层的分子比液体内部的分子有更大的分子势能 D.超声波可以在真空中传播
D.超声波可以在真空中传播
 注入人体,
注入人体, ⑶如图所示,质量分别为m1和m2的两个小球在光滑水平面上分别以速度v1、v2同向运动,并发生对心碰撞,碰后m2被右侧墙壁原速弹回,又与m1碰撞,再一次碰撞后两球都静止.求第一次碰后m1球速度的大小.
⑶如图所示,质量分别为m1和m2的两个小球在光滑水平面上分别以速度v1、v2同向运动,并发生对心碰撞,碰后m2被右侧墙壁原速弹回,又与m1碰撞,再一次碰撞后两球都静止.求第一次碰后m1球速度的大小.