题目内容
为了验证地面上物体的重力与地球吸引月球、太阳吸引行星的力是否为同一性质的力，遵循同样的规律，牛顿曾经做过著名的月-地检验，其基本想法是：如果重力和星体间的引力是同一性质的力，都与距离的 关系，因为月心到地心的距离是地球半径的60倍，那么月球绕地球做近似圆周运动的向心加速度就应该是地面重力加速度的 倍，牛顿通过计算证明他的想法是正确的．
【答案】分析：由圆周运动可算出向心加速度大小，再将月球做圆周运动的向心加速度与地球表面重力加速度进行比较，从而证明：重力和星体间的引力是同一性质的力．忽略地球自转的影响，根据万有引力等于重力列出等式；月球绕地球在引力提供向心力作用下做匀速圆周运动，从而可求出球绕地球运行的向心加速度与地球表面的重力加速度的之比．
解答：解：牛顿曾经做过著名的月-地检验，其基本想法是：如果重力和星体间的引力是同一性质的力，都与距离的二次方成反比关系．
物体在地球表面所受的重力等于其引力，则有：mg=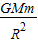
月球绕地球在引力提供向心力作用下做匀速圆周运动，则有：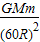
=man
联立上两式可得：an：g=1：3600
月球绕地球做近似圆周运动的向心加速度就应该是地面重力加速度的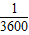
倍，
故答案为：二次方成反比，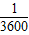
．
点评：万有引力定律通过理论进行科学、合理的推导，再由实际数据进行实践证明，从而进一步确定推导的正确性．
解答：解：牛顿曾经做过著名的月-地检验，其基本想法是：如果重力和星体间的引力是同一性质的力，都与距离的二次方成反比关系．
物体在地球表面所受的重力等于其引力，则有：mg=
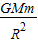
月球绕地球在引力提供向心力作用下做匀速圆周运动，则有：
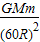=man联立上两式可得：an：g=1：3600
月球绕地球做近似圆周运动的向心加速度就应该是地面重力加速度的
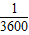倍，故答案为：二次方成反比，
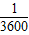．点评：万有引力定律通过理论进行科学、合理的推导，再由实际数据进行实践证明，从而进一步确定推导的正确性．
练习册系列答案
全优测试卷系列答案
冲刺100分1号卷系列答案
相关题目