题目内容
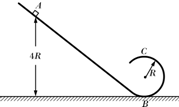如图所示，固定在竖直平面内的光滑轨道，由一段斜直轨道和与之相切的圆形轨道连接而成，圆形轨道半径为R．一质量为m的小物块（可视为质点）从斜直轨道上的A点由静止开始下滑，然后沿圆形轨道运动．A点距轨道最低点的竖直高度为4R．已知重力加速度为g．求：（1）小物块通过圆形轨道最高点C时速度v的大小；
（2）在最高点C时，轨道对小物块的作用力F的大小．
分析：对A到C过程运用机械能守恒定律，求出物体运动到C点的速度，根据重力和轨道弹力的合力提供向心力，结合牛顿第二定律求出轨道对物块的作用力大小．
解答：解：（1）根据机械能守恒定律有：mg×2R=
mv2
所以有：v=
=2
．
（2）根据牛顿第二定律有：mg+F=m
所以有：F=3mg
答：（1）小物块通过圆形轨道最高点C时速度v的大小为2
．
（2）轨道对小物块的作用力F的大小为3mg．
| 1 |
| 2 |
所以有：v=
| 4gR |
| gR |
（2）根据牛顿第二定律有：mg+F=m
| v2 |
| R |
所以有：F=3mg
答：（1）小物块通过圆形轨道最高点C时速度v的大小为2
| gR |
（2）轨道对小物块的作用力F的大小为3mg．
点评：本题考查了圆周运动和机械能守恒定律的综合，知道圆周运动向心力的来源是解决本题的关键．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
如图所示，固定在竖直平面半径为R的光滑圆环，有质量为m的小球在轨道内侧作圆周运动，小球恰好能通过圆环的最高点．已知重力加速度为g，则小球在运动过程（ ）
如图所示，固定在竖直平板且不可伸长的绝缘轻绳栓一质量为m、电量为q的小球（可视为点电荷），小球平衡时与固定在平板的点电荷Q的连线恰好水平．若小球的质量变为2m时，而其位置仍要保持不变，则小球的电量应该变为
计，g取10m/s2．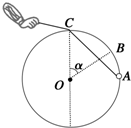
如图所示，固定在竖直平面内的半径为R=0.5m的光滑圆环的最高点C处有一个光滑的小孔，一质量为m=0.1kg的小球套在圆环上，一根细线的一端拴着这个小球，细线的另一端穿过小孔C，手拉细线使小球从A处沿圆环向上移动．在下列两种情况下，当小球通过B处，即∠COB=α=740时，求这两种情况下，细线对小球的拉力F的大小和圆环对小球的弹力FN的大小．（不计空气阻力，g取10m/s2；sin37°=0.6，cos37°=0.8；可能用到