题目内容
如图所示:一轻弹簧左端固定在足够长的木块A的左端挡板上,右端与小物块B连接,A、B及A与地面间的接触面均光滑.开始时,A和B均静止,现同时对A、B施加大小相等、方向相反的水平恒力F1和F2.则从两物体开始运动到以后的整个运动过程中(弹簧形变始终不超过其弹性限度),对A、B和弹簧组成的系统,正确的说法是( )
A.由于F1、F2大小相等、方向相反,故系统动量守恒
B.由于F1、F2大小相等、方向相反,故系统机械能守恒
C.当弹簧的弹力与F1、F2大小相等时,A、B的动能均达到最大值
D.当弹簧的形变量最大时,A、B均处于平衡状态
【答案】分析:正确解答本题需要掌握:动量守恒条件的应用;机械能守恒条件的理解以及如何求机械能的变化;正确应用牛顿第二定律分析AB的运动形式.
解答:解:对A、B和弹簧组成的系统所受合外力为零,因此系统动量守恒,故A正确;
由于F1、F2均对系统做正功,因此系统机械能不守恒,机械能增加,故B错误;
根据牛顿第二定律可知,开始A、B均做加速度逐渐减小的加速运动,当F1=F2=Kx时,A、B所受合外力均为零,此时二者速度最大,动能最大,然后开始做加速度逐渐增大的减速运动,当二者速度减为零时,弹簧最长,型变量最大,故C正确,D错误.
故选AC.
点评:本题考查了动量守恒、机械能守恒条件的理解以及牛顿第二定律的应用,注意正确理解这两种守恒的条件,同时正确对物体进行受力分析,明确运动状态变化.
解答:解:对A、B和弹簧组成的系统所受合外力为零,因此系统动量守恒,故A正确;
由于F1、F2均对系统做正功,因此系统机械能不守恒,机械能增加,故B错误;
根据牛顿第二定律可知,开始A、B均做加速度逐渐减小的加速运动,当F1=F2=Kx时,A、B所受合外力均为零,此时二者速度最大,动能最大,然后开始做加速度逐渐增大的减速运动,当二者速度减为零时,弹簧最长,型变量最大,故C正确,D错误.
故选AC.
点评:本题考查了动量守恒、机械能守恒条件的理解以及牛顿第二定律的应用,注意正确理解这两种守恒的条件,同时正确对物体进行受力分析,明确运动状态变化.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
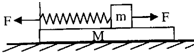 如图所示,一轻弹簧左端固定在表面光滑的长木板M的左端,右端与小物块m相连,静置于光滑水下地面上,弹簧处于原长状态.现同时对M利m施加等大、反向的水平恒力后,对M、m和弹簧组成的系统(弹簧的形变不超过弹性限度,木板足够长)正确的说法是( )
如图所示,一轻弹簧左端固定在表面光滑的长木板M的左端,右端与小物块m相连,静置于光滑水下地面上,弹簧处于原长状态.现同时对M利m施加等大、反向的水平恒力后,对M、m和弹簧组成的系统(弹簧的形变不超过弹性限度,木板足够长)正确的说法是( )| A、机械能守恒、动量守恒 | B、机械能守恒、动量不守恒 | C、机械能不守恒、动量不守恒 | D、机械能不守恒、动量守恒 |
 如图所示,一轻弹簧左端固定在长木板M的左端,右端与小木块m连接,且m与M及M与地面间接触光滑.开始时,m和M均静止,现同时对m、M施加等大反向的水平恒力F1和F2,从两物体开始运动以后的整个过程中,弹簧形变不超过弹弹性限度.对于m、M和弹簧组成的系统( )
如图所示,一轻弹簧左端固定在长木板M的左端,右端与小木块m连接,且m与M及M与地面间接触光滑.开始时,m和M均静止,现同时对m、M施加等大反向的水平恒力F1和F2,从两物体开始运动以后的整个过程中,弹簧形变不超过弹弹性限度.对于m、M和弹簧组成的系统( ) 如图所示,一轻弹簧左端固定,右端连结一物体A,物体处于光滑水平面上,弹簧处于原长,现用一向左恒力F推物体,则在物体向左运动至弹簧最短的过程中( )
如图所示,一轻弹簧左端固定,右端连结一物体A,物体处于光滑水平面上,弹簧处于原长,现用一向左恒力F推物体,则在物体向左运动至弹簧最短的过程中( )
 如图所示,一轻弹簧左端固定在长木板M的左端,右端与小木块m连接,且m、M及M与地面间摩擦不计.开始时m和M均静止,现同时对m、M施加等大反向的水平恒力F1和F2,设两物体开始运动以后的整个运动过程中,弹簧形变不超过其弹性限度.对于m、M和弹簧组成的系统( )
如图所示,一轻弹簧左端固定在长木板M的左端,右端与小木块m连接,且m、M及M与地面间摩擦不计.开始时m和M均静止,现同时对m、M施加等大反向的水平恒力F1和F2,设两物体开始运动以后的整个运动过程中,弹簧形变不超过其弹性限度.对于m、M和弹簧组成的系统( )