题目内容
将卫星发射至近地圆轨道1(如图所示),然后再次点火,将卫星送入同步轨道3.轨道1、2相切于Q点,2、3相切于P点,则当卫星分别在1、2、3轨道上正常运行时,以下说法正确的是( )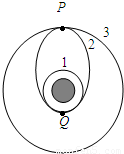
A.卫星在轨道3上的速度大于轨道1上的速度
B.卫星在轨道3上的角速度大于在轨道1上的角速度
C.卫星在轨道2上经过Q点时的速度大于它在轨道2上经过P点时的速度
D.卫星在轨道2上经过P点的加速度等于它在轨道3上经过P点时的加速度
【答案】分析:根据人造卫星的万有引力等于向心力,列式求出线速度、角速度表达式进行讨论即可.
当万有引力刚好提供卫星所需向心力时 卫星正好可以做匀速圆周运动
1.若是供大于需 则卫星做逐渐靠近圆心的运动
2.若是供小于需 则卫星做逐渐远离圆心的运动
解答:解:由万有引力提供向心力,根据牛顿第二定律得:G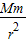 =ma=mω2r=m
=ma=mω2r=m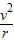 =①,
=①,
A、由①解得,v=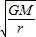 ,卫星在轨道3上的速度小于轨道1上的速度,故A错误
,卫星在轨道3上的速度小于轨道1上的速度,故A错误
B、由①解得,ω=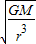 ,卫星在轨道3上的角速度小于在轨道1上的角速度,故B错误
,卫星在轨道3上的角速度小于在轨道1上的角速度,故B错误
C、因为卫星在轨道上飞行只受引力,根据机械能守恒条件知道,
卫星在椭圆轨道上飞行时机械能守恒,由于远地点P的势能大于近地点Q势能,所以远地点P的动能就小于近地点Q的动能.所以卫星在轨道2上经过Q点时的速度大于它在轨道2上经过P点时的速度,故C正确
D、由①解得,a=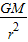 ,所以卫星在轨道2上经过P点的加速度等于它在轨道3上经过P点时的加速度.故D正确
,所以卫星在轨道2上经过P点的加速度等于它在轨道3上经过P点时的加速度.故D正确
故选CD.
点评:本题关键抓住万有引力提供向心力,先列式求解出线速度和角速度的表达式,再进行讨论.
当万有引力刚好提供卫星所需向心力时 卫星正好可以做匀速圆周运动
1.若是供大于需 则卫星做逐渐靠近圆心的运动
2.若是供小于需 则卫星做逐渐远离圆心的运动
解答:解:由万有引力提供向心力,根据牛顿第二定律得:G
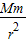 =ma=mω2r=m
=ma=mω2r=m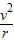 =①,
=①,A、由①解得,v=
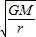 ,卫星在轨道3上的速度小于轨道1上的速度,故A错误
,卫星在轨道3上的速度小于轨道1上的速度,故A错误B、由①解得,ω=
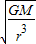 ,卫星在轨道3上的角速度小于在轨道1上的角速度,故B错误
,卫星在轨道3上的角速度小于在轨道1上的角速度,故B错误C、因为卫星在轨道上飞行只受引力,根据机械能守恒条件知道,
卫星在椭圆轨道上飞行时机械能守恒,由于远地点P的势能大于近地点Q势能,所以远地点P的动能就小于近地点Q的动能.所以卫星在轨道2上经过Q点时的速度大于它在轨道2上经过P点时的速度,故C正确
D、由①解得,a=
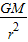 ,所以卫星在轨道2上经过P点的加速度等于它在轨道3上经过P点时的加速度.故D正确
,所以卫星在轨道2上经过P点的加速度等于它在轨道3上经过P点时的加速度.故D正确故选CD.
点评:本题关键抓住万有引力提供向心力,先列式求解出线速度和角速度的表达式,再进行讨论.

练习册系列答案
相关题目
 发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3,轨道1、2相切于Q点,轨道2、3相切于P点,如图所示.已知地球半径为R,同步轨道3距地面的高度为6R,地球自转周期为T,卫星在近地圆轨道上运行周期为T0,万有引力常数为G.则下列说法正确的是( )
发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3,轨道1、2相切于Q点,轨道2、3相切于P点,如图所示.已知地球半径为R,同步轨道3距地面的高度为6R,地球自转周期为T,卫星在近地圆轨道上运行周期为T0,万有引力常数为G.则下列说法正确的是( )


