题目内容
1. 回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电极相连接的两个D形金属盒,两盒间的狭缝中形成的周期变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底面的匀强磁场,D形盒中央为质子流,D形盒的交流电压为U,静止质子经电场加速后,进入D形盒,其最大轨道半径为R,磁场的磁感应强度为B,质子质量为m,电荷量为q,求:
回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电极相连接的两个D形金属盒,两盒间的狭缝中形成的周期变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底面的匀强磁场,D形盒中央为质子流,D形盒的交流电压为U,静止质子经电场加速后,进入D形盒,其最大轨道半径为R,磁场的磁感应强度为B,质子质量为m,电荷量为q,求:(1)交流电源的频率是多少.
(2)质子经回旋加速器最后得到的最大动能多大;
(3)质子在D型盒内运动的总时间t(狭缝宽度小于R,质子在狭缝中运动时间不计)
分析 (1)粒子在磁场中运动,洛伦兹力提供向心力,然后结合$T=\frac{2πr}{v}$即可求出周期,由f=$\frac{1}{T}$求出频率;
(2)设粒子的最大速度为vm,对应着粒子的最大运动半径即R,由洛伦兹力提供向心力即可求出粒子的最大动能;
(3)质子在每一个周期内两次经过电场,即每一个周期内电场对质子加速两次,根据动能定理求出质子加速的次数,然后结合最大动能即可求出.
解答 解:(1)质子在磁场中运动,洛伦兹力提供向心力,设质子的速度为v,则:qBv=m$\frac{{v}^{2}}{R}$,
解得:v=$\frac{qBR}{m}$,
根据T=$\frac{2πR}{v}$,f=$\frac{1}{T}$
得:T=$\frac{2πm}{qB}$,f=$\frac{qB}{2πm}$
(2)质子的最大运动半径即R,由:$q{v}_{m}B=\frac{m{v}_{m}^{2}}{R}$
则有最大动能为:EKm=$\frac{1}{2}m{v}_{m}^{2}$=$\frac{1}{2}×m×(\frac{qBR}{m})^{2}$=$\frac{{q}^{2}{B}^{2}{R}^{2}}{2m}$.
(3)质子在每一个周期内两次经过电场,即每一个周期内电场对质子加速两次,设需要经过n次加速粒质子的动能达到最大,则:
$n•qU=\frac{{q}^{2}{B}^{2}{R}^{2}}{2m}$
所以质子在D型盒内运动的总时间:t=$\frac{n}{2}•T$
联立方程得:t=$\frac{π{R}^{2}B}{2U}$
答:(1)交流电源的频率是$\frac{qB}{2πm}$.
(2)质子经回旋加速器最后得到的最大动能是$\frac{{q}^{2}{B}^{2}{R}^{2}}{2m}$;
(3)质子在D型盒内运动的总时间是$\frac{π{R}^{2}B}{2U}$.
点评 解决本题的关键知道回旋加速器运用电场加速,磁场偏转来加速带电粒子,但要注意粒子射出的速度与加速电压无关,与磁感应强度的大小和D型盒半径有关.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案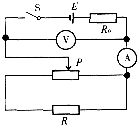 如图所示为一直流电路,电源内阻小于R0,滑动变阻器的最大阻值小于R.在滑动变阻器的滑片P从最右端滑向最左端的过程中,下列说法错误的是( )
如图所示为一直流电路,电源内阻小于R0,滑动变阻器的最大阻值小于R.在滑动变阻器的滑片P从最右端滑向最左端的过程中,下列说法错误的是( )| A. | 电压表的示数一直增大 | B. | 电流表的示数一直增大 | ||
| C. | 电阻R0消耗的功率一直增大 | D. | 电源的输出功率先减小后增大 |
 回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电源两极相连接的两个D形金属盒,两盒间的狭缝中形成周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示.设D形盒半径为R.若用回旋加速器加速质子时,匀强磁场的磁感应强度为B,高频交流电频率为f.则下列说法正确的是( )
回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电源两极相连接的两个D形金属盒,两盒间的狭缝中形成周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示.设D形盒半径为R.若用回旋加速器加速质子时,匀强磁场的磁感应强度为B,高频交流电频率为f.则下列说法正确的是( )| A. | 质子被加速后的最大速度不可能超过2πfR | |
| B. | 质子被加速后的最大速度与加速电场的电压大小有关 | |
| C. | 高频电源只能使用矩形交变电流,不能使用正弦式交变电流 | |
| D. | 不改变B和f,该回旋加速器也能用于加速α粒子 |
 如图所示,直流电源电动势为E,内阻为r,R1、R2为定值电阻,且R1>r,R为滑动变阻器,G为灵敏电流计,电容器中一个带电微粒恰处于平衡状态,则( )
如图所示,直流电源电动势为E,内阻为r,R1、R2为定值电阻,且R1>r,R为滑动变阻器,G为灵敏电流计,电容器中一个带电微粒恰处于平衡状态,则( )| A. | 当R的滑动触头向下滑动时,回路总电流变小 | |
| B. | 当R的滑动触头向下滑动时,电流计中电流方向a→b | |
| C. | 当R的滑动触头向上滑动时,微粒将向下移动 | |
| D. | 当R的滑动触头向上滑动时,电源输出功率将减小 |
 如图所示,质量为10kg的物体A拴在一个被水平拉伸的弹簧一端,弹簧的拉力为5N时,物体A处于静止状态.若小车以1m/s2的加速度向右运动稳定后( )
如图所示,质量为10kg的物体A拴在一个被水平拉伸的弹簧一端,弹簧的拉力为5N时,物体A处于静止状态.若小车以1m/s2的加速度向右运动稳定后( )| A. | 物体A仍相对小车静止 | |
| B. | 物体A受到的摩擦力减小 | |
| C. | 物体A受到的弹力增大 | |
| D. | 物体A受到的摩擦力大小不变,但方向改变 |

(1)图乙为某次实验得到的纸带的一部分,已知交流电的频率为50Hz,根据纸带可求出小车的加速度大小为3.19m/s2(结果保留三位有效数字).
(2)保持砂和砂桶质量不变,改变小车质量,得到数据如下表格,图丙是依据表格数据描出了相应的点.根据这些点画出a-$\frac{1}{m}$图线,由图线写出小车加速度与质量倒数之间的关系式是a=$\frac{1}{2m}$.
| 实验次数 物理量 | 1 | 2 | 3 | 4 | 5 | 6 |
| 小车加速度a/m•s-2 | 1.50 | 1.25 | 1.00 | 0.75 | 0.50 | 0.30 |
| 小车质量m/kg | 0.33 | 0.40 | 0.50 | 0.71 | 1.00 | 1.67 |
| $\frac{1}{m}$/kg-1 | 3.03 | 2.50 | 2.00 | 1.25 | 1.00 | 0.60 |
 如图所示,一足够长的固定光滑斜面倾角为θ=37°,两物块A、B的质量分别为mA=1kg、mB=4kg,两物块用长为L=12.5cm轻绳相连,轻绳可承受的最大拉力为T=12N,对B施加一沿斜面向上的力F,使A、B由静止开始一起向上运动,力F逐渐增大,g取10m/s2(sin37°=0.6,cos37°=0.8).
如图所示,一足够长的固定光滑斜面倾角为θ=37°,两物块A、B的质量分别为mA=1kg、mB=4kg,两物块用长为L=12.5cm轻绳相连,轻绳可承受的最大拉力为T=12N,对B施加一沿斜面向上的力F,使A、B由静止开始一起向上运动,力F逐渐增大,g取10m/s2(sin37°=0.6,cos37°=0.8).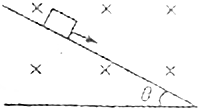 如图所示,一光滑、绝缘斜面,倾角θ=37°,一质量m=0.02kg的物体(可视为质点)从斜面上的某点由静止开始下滑.如果物体的带电量q=+10-2C,垂直纸面向里的匀强磁场B=4.0T.试求:物体在斜面上运动的最大速率及沿斜面下滑的最大距离(g取10m/s2,sin37°=0.6,cos37°=0.8,斜面足够长).
如图所示,一光滑、绝缘斜面,倾角θ=37°,一质量m=0.02kg的物体(可视为质点)从斜面上的某点由静止开始下滑.如果物体的带电量q=+10-2C,垂直纸面向里的匀强磁场B=4.0T.试求:物体在斜面上运动的最大速率及沿斜面下滑的最大距离(g取10m/s2,sin37°=0.6,cos37°=0.8,斜面足够长).
