题目内容
17.质量为m,电荷量为q的质点,在静电力作用下以恒定速率v沿圆弧由A运动到B,其速度方向改变θ角,AB弧长为s,则A、B两点的电势差UAB=0,AB中点的场强大小E=$\frac{m{v}^{2}θ}{qs}$.分析 由题意知电荷在静电力作用下做的是匀速圆周运动,静电力做的功是零得出A、B两点间的电势差.
静电力是质点做圆周运动的向心力列出等式和点电荷的场强公式结合求解AB弧中点的场强大小.
解答 解:由题意知电荷在静电力作用下做的是匀速圆周运动,从A点运动到B点,
由动能定理知,静电力做的功是零,
所以A、B两点间的电势差UAB=0
设场源电荷的电荷量为Q,质点做圆周运动的轨道半径为r,则弧长s=θr ①
静电力是质点做圆周运动的向心力,即$\frac{kQq}{{r}^{2}}=\frac{m{v}^{2}}{r}$ ②
弧AB中点的场强大小E=$\frac{kQ}{{r}^{2}}$ ③
解①②③组成的方程组得E=$\frac{m{v}^{2}θ}{qs}$
故答案为:0;$\frac{m{v}^{2}θ}{qs}$
点评 涉及到电势差的问题,常常要用到动能定理.要掌握电场强度,电势差,电场力做功等物理量间的关系.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
7.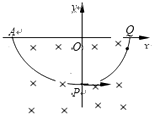 如图所示,xOy平面直角坐标系的第三和第四象限均存在垂直平面向里的匀强磁场,第四象限还存在与y轴平行的匀强电场.一带电小球从x轴上的A点由静止释放,恰好从P点垂直于y 轴进入第四象限,然后做圆周运动,从Q点垂直于x轴进入第一象限,Q点距O点的距离为d,重力加速度为g,根据以上信息,可以判断( )
如图所示,xOy平面直角坐标系的第三和第四象限均存在垂直平面向里的匀强磁场,第四象限还存在与y轴平行的匀强电场.一带电小球从x轴上的A点由静止释放,恰好从P点垂直于y 轴进入第四象限,然后做圆周运动,从Q点垂直于x轴进入第一象限,Q点距O点的距离为d,重力加速度为g,根据以上信息,可以判断( )
 如图所示,xOy平面直角坐标系的第三和第四象限均存在垂直平面向里的匀强磁场,第四象限还存在与y轴平行的匀强电场.一带电小球从x轴上的A点由静止释放,恰好从P点垂直于y 轴进入第四象限,然后做圆周运动,从Q点垂直于x轴进入第一象限,Q点距O点的距离为d,重力加速度为g,根据以上信息,可以判断( )
如图所示,xOy平面直角坐标系的第三和第四象限均存在垂直平面向里的匀强磁场,第四象限还存在与y轴平行的匀强电场.一带电小球从x轴上的A点由静止释放,恰好从P点垂直于y 轴进入第四象限,然后做圆周运动,从Q点垂直于x轴进入第一象限,Q点距O点的距离为d,重力加速度为g,根据以上信息,可以判断( )| A. | 电荷的正负 | B. | 电场强度的大小和方向 | ||
| C. | 磁感应强度大小 | D. | 小球在第四象限运动的时间 |
8.下列关于波的说法中正确的是( )
| A. | 在给定的介质中传播时,振幅越大,则波传播的速度越快 | |
| B. | 波源振动的频率越高,则波传播一个波长的距离所用的时间越长 | |
| C. | 在一个周期内,振动质点走过的路程等于一个波长 | |
| D. | 多普勒效应是由于波源与观察者之间有相对运动而产生的 |
5. 如图所示,一物体从圆弧形轨道的A点无初速滑下,物体与圆弧轨道间的动摩擦因数为μ,由于摩擦力的作用物体沿轨道到达C点时的速度为零,C点比A点下降了h1,物体又由C点沿轨道滑至B点,速度再次为零,B比C下降了h2,则h1与h2比较有( )
如图所示,一物体从圆弧形轨道的A点无初速滑下,物体与圆弧轨道间的动摩擦因数为μ,由于摩擦力的作用物体沿轨道到达C点时的速度为零,C点比A点下降了h1,物体又由C点沿轨道滑至B点,速度再次为零,B比C下降了h2,则h1与h2比较有( )
 如图所示,一物体从圆弧形轨道的A点无初速滑下,物体与圆弧轨道间的动摩擦因数为μ,由于摩擦力的作用物体沿轨道到达C点时的速度为零,C点比A点下降了h1,物体又由C点沿轨道滑至B点,速度再次为零,B比C下降了h2,则h1与h2比较有( )
如图所示,一物体从圆弧形轨道的A点无初速滑下,物体与圆弧轨道间的动摩擦因数为μ,由于摩擦力的作用物体沿轨道到达C点时的速度为零,C点比A点下降了h1,物体又由C点沿轨道滑至B点,速度再次为零,B比C下降了h2,则h1与h2比较有( )| A. | h1>h2 | B. | h1<h2 | C. | h1=h2 | D. | 无法确定 |
12. 如图所示,一轻质弹簧一端系在墙上的O点,自由伸长到B点.今用一小物体m把弹簧压缩到A点,然后释放,小物体能运动到C点静止,物体与水平地面间的动摩擦因数恒定,试判断下列说法正确的是( )
如图所示,一轻质弹簧一端系在墙上的O点,自由伸长到B点.今用一小物体m把弹簧压缩到A点,然后释放,小物体能运动到C点静止,物体与水平地面间的动摩擦因数恒定,试判断下列说法正确的是( )
 如图所示,一轻质弹簧一端系在墙上的O点,自由伸长到B点.今用一小物体m把弹簧压缩到A点,然后释放,小物体能运动到C点静止,物体与水平地面间的动摩擦因数恒定,试判断下列说法正确的是( )
如图所示,一轻质弹簧一端系在墙上的O点,自由伸长到B点.今用一小物体m把弹簧压缩到A点,然后释放,小物体能运动到C点静止,物体与水平地面间的动摩擦因数恒定,试判断下列说法正确的是( )| A. | 物体从A到B速度越来越大,从B到C速度越来越小 | |
| B. | 物体从A到B速度越来越小,从B到C加速度不变 | |
| C. | 物体从A到B先加速后减速,从B一直减速运动 | |
| D. | 物体在B点受到的合外力为零 |
2.(多选)人握住旗杆匀速上爬,则下列说法正确的是( )
| A. | 人受到的摩擦力的方向是沿杆向下的 | |
| B. | 人受到的摩擦力的方向是沿杆向上的 | |
| C. | 人握旗杆用力越大,人受的摩擦力也越大 | |
| D. | 人握旗杆用力越大,并不会使人受的摩擦力增大 |
2.下列说法正确的是( )
| A. | 力和位移都是矢量,所以功也是矢量 | |
| B. | 正功大于负功 | |
| C. | 人能够搬动重物做功,说明人具有能量 | |
| D. | 机械效率高,表示机械做功快 |
3.边长为L的正方形闭合线圈共n匝,在磁感应强度为B的匀强磁场中以角速度ω绕垂直于磁感线并在线圈平面内的轴匀速转动,要使线圈中的感应电流增大1倍,下列措施不可采用的是( )
| A. | 只将角速度ω增大1倍 | B. | 只将线圈边长L增大至2L | ||
| C. | 只将线圈匝数增加至2n | D. | 只将磁感应强度增至2B |
 如图所示为皮带传动装置,左轮O1是一个轮轴,大轮半径为R1,小轮半径为R2,A、B分别是大轮和小轮边缘上的点,右轮O2的半径为R3,C是右轮边缘上的点,已知R1:R2:R3=3:2:1,转动中皮带不打滑.
如图所示为皮带传动装置,左轮O1是一个轮轴,大轮半径为R1,小轮半径为R2,A、B分别是大轮和小轮边缘上的点,右轮O2的半径为R3,C是右轮边缘上的点,已知R1:R2:R3=3:2:1,转动中皮带不打滑.