题目内容
 如图所示,a、b、c、d为4个正离子,电荷量相等均为q,同时沿图示方向进入速度选择器后,a粒子射向P1板,b粒子射向P2板,c、d两粒子通过速度选择器后,进入另一磁感应强度为B2的磁场,分别打在A1和A2两点,A1和A2两点相距△x.已知速度选择器两板电压为U,两板距离为d,板间磁感应强度为B1
如图所示,a、b、c、d为4个正离子,电荷量相等均为q,同时沿图示方向进入速度选择器后,a粒子射向P1板,b粒子射向P2板,c、d两粒子通过速度选择器后,进入另一磁感应强度为B2的磁场,分别打在A1和A2两点,A1和A2两点相距△x.已知速度选择器两板电压为U,两板距离为d,板间磁感应强度为B1(1)试判断a、b、c、d四粒子进入速度选择器的速度va、vb、vc、vd大小关系.(用<、>或=表示)
(2)试求出vc、vd,
(3)试判断c、d粒子的质量mc 与md是否相等,若不等,求出它们的质量差△m.
分析:1、粒子进入速度选择器,只有满足qvB=qE,即速度满足v=
,才能通过速度选择器,不发生偏转.当粒子的速度大于
,洛伦兹力大于电场力,粒子向右偏转,当粒子的速度小于
,洛伦兹力小于电场力,粒子向左偏转.
2、由于c、d不偏转,故满足电场力等于洛伦兹力Eq=Bqv,即:
q=B1qv,化简可得c、d的速度.
3、c、d进入磁场中做圆周运动,洛伦兹力提供向心力qvB2=m
得R=
,由于Rc<Rd,故mc<md.根据几何关系△x=2(Rd-Rc)=2(
-
),把c、d的速度值代入,化简得它们的质量差△m.
| E |
| B |
| E |
| B |
| E |
| B |
2、由于c、d不偏转,故满足电场力等于洛伦兹力Eq=Bqv,即:
| U |
| d |
3、c、d进入磁场中做圆周运动,洛伦兹力提供向心力qvB2=m
| v2 |
| R |
| mv |
| qB2 |
| mdvd |
| qB2 |
| mcvc |
| qB2 |
解答:解:(1)粒子进入速度选择器,只有满足qvB=qE,即速度满足v=
,才能通过速度选择器,不发生偏转.
当粒子的速度大于
,洛伦兹力大于电场力,粒子向右偏转,
当粒子的速度小于
,洛伦兹力小于电场力,粒子向左偏转.
故va<vc=vd<vb
(2)c、d不偏转,故满足电场力等于洛伦兹力Eq=Bqv
即:
q=B1qv
得,vc=vd=
(3)c、d进入磁场中做圆周运动,洛伦兹力提供向心力qvB2=m
得R=
由于Rc<Rd,故mc<md.
c、d两粒子分别打在A1和A2两点,A1和A2两点相距△x.根据几何关系得:
△x=2(Rd-Rc)=2(
-
)
把vc=vd=
代入上式中,化简得
△m=md-mc=
答:(1)a、b、c、d四粒子进入速度选择器的速度va、vb、vc、vd大小关系为va<vc=vd<vb.
(2)vc=vd=
.
(3)c、d粒子的质量mc 与md不相等,它们的质量差△m为
.
| E |
| B |
当粒子的速度大于
| E |
| B1 |
当粒子的速度小于
| E |
| B1 |
故va<vc=vd<vb
(2)c、d不偏转,故满足电场力等于洛伦兹力Eq=Bqv
即:
| U |
| d |
得,vc=vd=
| U |
| dB1 |
(3)c、d进入磁场中做圆周运动,洛伦兹力提供向心力qvB2=m
| v2 |
| R |
得R=
| mv |
| qB2 |
由于Rc<Rd,故mc<md.
c、d两粒子分别打在A1和A2两点,A1和A2两点相距△x.根据几何关系得:
△x=2(Rd-Rc)=2(
| mdvd |
| qB2 |
| mcvc |
| qB2 |
把vc=vd=
| U |
| dB1 |
△m=md-mc=
| B1B2dq△x |
| 2U |
答:(1)a、b、c、d四粒子进入速度选择器的速度va、vb、vc、vd大小关系为va<vc=vd<vb.
(2)vc=vd=
| U |
| dB1 |
(3)c、d粒子的质量mc 与md不相等,它们的质量差△m为
| B1B2dq△x |
| 2U |
点评:本题关键是要能判断在速度选择器中四个粒子的速度大小关系,带电粒子进入速度选择器,只有满足qvB=qE,即速度满足v=
,才能通过速度选择器,不发生偏转.当粒子的速度大于
,洛伦兹力大于电场力,粒子向右偏转,当粒子的速度小于
,洛伦兹力小于电场力,粒子向左偏转.
| E |
| B |
| E |
| B |
| E |
| B |

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目

 如图所示,a、b、c为电场中同一电场线上的三点,且b为ac的中点,a、c电势分别为φa=8V,φc=6V.下列叙述正确的是( )
如图所示,a、b、c为电场中同一电场线上的三点,且b为ac的中点,a、c电势分别为φa=8V,φc=6V.下列叙述正确的是( ) 如图所示,A、B、C、D是某匀强电场中的4个等势面,一个质子和一个α粒子(电荷量是质子的2倍,质量是质子的4倍)同时在A等势面从静止出发,向右运动,当到达D等势面时,下列说法正确的是( )
如图所示,A、B、C、D是某匀强电场中的4个等势面,一个质子和一个α粒子(电荷量是质子的2倍,质量是质子的4倍)同时在A等势面从静止出发,向右运动,当到达D等势面时,下列说法正确的是( ) 如图所示,a、b和c都是厚度均匀的平玻璃板,a和b、b和c之间的夹角都为α,一细光束由红光和蓝光组成,以入射角θ从O点射入a板,且射出c板后的两束单色光通过空气射在地面上P、Q两点,由此可知( )
如图所示,a、b和c都是厚度均匀的平玻璃板,a和b、b和c之间的夹角都为α,一细光束由红光和蓝光组成,以入射角θ从O点射入a板,且射出c板后的两束单色光通过空气射在地面上P、Q两点,由此可知( )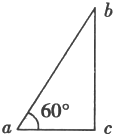 如图所示,a、b、c是匀强电场中的直角三角形的三个顶点.已知a、b、c三点的电势分别为φa=8V、φb=-4V、φc=2V,
如图所示,a、b、c是匀强电场中的直角三角形的三个顶点.已知a、b、c三点的电势分别为φa=8V、φb=-4V、φc=2V,