题目内容
 如图所示,在xOy坐标系的第Ⅰ象限内存在垂直纸面向外的匀强磁场,磁感应强度为B,在x>0轴上有一平面荧光屏,在y轴上距坐标原点O为L的S处有一粒子源,在某时刻同时发射大量质量为m、电荷量为q的带正电粒子,它们的速度大小相同,速度方向均在xy平面内,与y轴正方向的夹角分布在0~180°范围内.观察发现:荧光屏OP之间发光,P点右侧任何位置均不发光,在P、Q之间的任一位置会先后二次发光;O、Q之间的任一位置只有一次发光,测出O、P间距为
如图所示,在xOy坐标系的第Ⅰ象限内存在垂直纸面向外的匀强磁场,磁感应强度为B,在x>0轴上有一平面荧光屏,在y轴上距坐标原点O为L的S处有一粒子源,在某时刻同时发射大量质量为m、电荷量为q的带正电粒子,它们的速度大小相同,速度方向均在xy平面内,与y轴正方向的夹角分布在0~180°范围内.观察发现:荧光屏OP之间发光,P点右侧任何位置均不发光,在P、Q之间的任一位置会先后二次发光;O、Q之间的任一位置只有一次发光,测出O、P间距为| 3 |
(1)粒子发射时的速度大小;
(2)Q点先后发光的时间间隔.
分析:(1)根据洛伦兹力提供向心力,使其做匀速圆周运动,并由最长的弦是圆的直径,并结合几何关系可得出粒子的速度大小;
(2)根据题意可分劣圆弧与优圆弧,从而由几何关系来确定已知长度与半径的关系,并由周期公式可求出Q点先后发光的时间间隔.
(2)根据题意可分劣圆弧与优圆弧,从而由几何关系来确定已知长度与半径的关系,并由周期公式可求出Q点先后发光的时间间隔.
解答:解:(1)由于洛伦兹力提供向心力,根据qvB=m
,
解得:v=
所以每个粒子在匀强磁场中做圆周运动,半径相同.而x轴的任一亮点与S的连线为圆的弦长,由于P点是粒子到达x轴上最远点,
因此SP的连线为圆的最大弦长,即圆的直径.则
=2r,
根据几何关系:
2=
2+
2
解得r=L
∵L=
∴v=
(2)aS连线与SP连线垂直,在∠aSO范围内发射粒子运动一段劣圆弧可以到达OP间任何一位置,
在∠aSy范围内发射粒子运动一段优圆弧能到达OP间任何一位置,设粒子发射方向与y轴成θ角时,运动圆轨迹恰好与x轴的Q点相切.
根据几何关系,L=r+rsinθ
=rcosθ
∵θ=0°
=L
∴t=
∵粒子沿优圆弧运动到达Q点的时间t2=
粒子沿劣圆弧运动到达Q点的时间t1=
∴△t=t2-t1=
答:(1)粒子发射时的速度大小
;
(2)Q点先后发光的时间间隔
.
| v2 |
| r |
解得:v=
| mr |
| Bq |
所以每个粒子在匀强磁场中做圆周运动,半径相同.而x轴的任一亮点与S的连线为圆的弦长,由于P点是粒子到达x轴上最远点,
因此SP的连线为圆的最大弦长,即圆的直径.则
. |
| SP |
根据几何关系:
. |
| SP |
. |
| OS |
. |
| OP |
解得r=L
∵L=
| mv |
| Bq |
∴v=
| BLq |
| m |
(2)aS连线与SP连线垂直,在∠aSO范围内发射粒子运动一段劣圆弧可以到达OP间任何一位置,
在∠aSy范围内发射粒子运动一段优圆弧能到达OP间任何一位置,设粒子发射方向与y轴成θ角时,运动圆轨迹恰好与x轴的Q点相切.
根据几何关系,L=r+rsinθ
. |
| OQ |
∵θ=0°
. |
| OQ |
∴t=
| Mθ |
| Bq |
∵粒子沿优圆弧运动到达Q点的时间t2=
| 3πm |
| 2qB |
粒子沿劣圆弧运动到达Q点的时间t1=
| πm |
| 2qB |
∴△t=t2-t1=
| πm |
| qB |
答:(1)粒子发射时的速度大小
| BLq |
| m |
(2)Q点先后发光的时间间隔
| πm |
| qB |
点评:考查牛顿第二定律,向心力公式,并突出几何关系在本题的应用,同时注重对运动轨迹的分析,利用圆的特性来解题是本题的突破口.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 如图所示,在竖直平面的xOy坐标系中,Oy竖直向上,Ox水平.设平面内存在沿x轴正方向的恒定风力.一物体从坐标原点沿Oy方向竖直向上抛出,初速度为v0=4m/s,不计空气阻力,到达最高点的位置如图中M点所示,(坐标格为正方形,g=10m/s2)
如图所示,在竖直平面的xOy坐标系中,Oy竖直向上,Ox水平.设平面内存在沿x轴正方向的恒定风力.一物体从坐标原点沿Oy方向竖直向上抛出,初速度为v0=4m/s,不计空气阻力,到达最高点的位置如图中M点所示,(坐标格为正方形,g=10m/s2) 如图所示,在竖直平面的xoy坐标系中,oy竖直向上,ox水平.该平面内存在沿x轴正方向的恒定风力.一物体从坐标原点沿oy方向竖直向上抛出,初速度为V0=4m/s,不计空气阻力,到达最高点的位置如图中M点所示,(坐标格为正方形)求:
如图所示,在竖直平面的xoy坐标系中,oy竖直向上,ox水平.该平面内存在沿x轴正方向的恒定风力.一物体从坐标原点沿oy方向竖直向上抛出,初速度为V0=4m/s,不计空气阻力,到达最高点的位置如图中M点所示,(坐标格为正方形)求: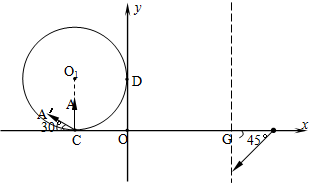 D点进入电场,最后从G点以与x轴正向夹角为45°的方向射出电场.求:
D点进入电场,最后从G点以与x轴正向夹角为45°的方向射出电场.求:
