题目内容
匀强电场的方向沿x轴正向,电场强度E随x的分布如图所示.图中E0和d均为已知量,将带正电的质点A在O点由能止释放,A离开电场足够远后,再将另一带正电的质点B放在O点也由静止释放,当B在电场中运动时,A、B间的相互作用力及相互作用能均为零;B离开电场后,A、B间的相作用视为静电作用,已知A的电荷量为Q,A和B的质量分别为m和
,不计重力.
(1)求A在电场中的运动时间t;
(2)若B的电荷量q=
Q,求两质点相互作用能的最大值EPm;
(3)为使B离开电场后不改变运动方向,求B所带电荷量的最大值qm.
| m |
| 4 |
(1)求A在电场中的运动时间t;
(2)若B的电荷量q=
| 4 |
| 9 |
(3)为使B离开电场后不改变运动方向,求B所带电荷量的最大值qm.

(1)由牛顿第二定律,A在电场中运动的加速a=
=
A在电场中做匀变速直线运动 d=
at2
解得运动时间t=
=
(2)设A.B离开电场的速度分别为vA0、vB0,由动能定理,有
QEOd=
m
,qE0d=
?
?
①
A、B相互作用的过程中,动量和能量均守恒,A、B间相互作用力为斥力,A受力方向与其运动方向相同,B受力方向与其运动方向相反,相互作用力A做正功,对B做负功.在AB靠近的过程中,B的路程大于A的路程,由于作用力大小相等,作用力对B做功的绝对值大于对A做功的绝对值,因此相互作用力做功之和为负,相互作用能增加,所以当A、B最接近时,相互作用能最大,因此两者速度相同,设v′,有
(m+
)v′=mvA0+
vB0 ②
Epm=(
m
+
?
?
)-
(m+
)v′2 ③
又已知 q=
Q,由①②③解得 相互作用能的最大值为 Epm=
QE0d
(3)考虑A、B在x>d区间的运动,由动量守恒、能量守恒,且在初态和末态均无相互作用,有
mvA+
vB=mvA0+
vB0 ④
m
+
?
?
=
m
+
?
?
⑤
由④⑤解得 vB=-
vB0+
vA0
因B不改变运动方向,故vB≥0 ⑥
由①⑥解得 q≤
Q
即B所带电荷量的最大值为 Qm=
Q
答:(1)求A在电场中的运动时间t是
;
(2)若B的电荷量q=
Q,两质点相互作用能的最大值EPm是
QE0d.
(3)为使B离开电场后不改变运动方向,B所带电荷量的最大值qm是
Q.
| f |
| m |
| QE0 |
| m |
A在电场中做匀变速直线运动 d=
| 1 |
| 2 |
解得运动时间t=
|
|
(2)设A.B离开电场的速度分别为vA0、vB0,由动能定理,有
QEOd=
| 1 |
| 2 |
| v | 2A0 |
| 1 |
| 2 |
| m |
| 4 |
| v | 2B0 |
A、B相互作用的过程中,动量和能量均守恒,A、B间相互作用力为斥力,A受力方向与其运动方向相同,B受力方向与其运动方向相反,相互作用力A做正功,对B做负功.在AB靠近的过程中,B的路程大于A的路程,由于作用力大小相等,作用力对B做功的绝对值大于对A做功的绝对值,因此相互作用力做功之和为负,相互作用能增加,所以当A、B最接近时,相互作用能最大,因此两者速度相同,设v′,有
(m+
| m |
| 4 |
| m |
| 4 |
Epm=(
| 1 |
| 2 |
| v | 2A0 |
| 1 |
| 2 |
| m |
| 4 |
| v | 2B0 |
| 1 |
| 2 |
| m |
| 4 |
又已知 q=
| 4 |
| 9 |
| 1 |
| 45 |
(3)考虑A、B在x>d区间的运动,由动量守恒、能量守恒,且在初态和末态均无相互作用,有
mvA+
| m |
| 4 |
| m |
| 4 |
| 1 |
| 2 |
| v | 2A |
| 1 |
| 2 |
| m |
| 4 |
| v | 2B |
| 1 |
| 2 |
| v | 2A0 |
| 1 |
| 2 |
| m |
| 4 |
| v | 2B0 |
由④⑤解得 vB=-
| 3 |
| 5 |
| 8 |
| 5 |
因B不改变运动方向,故vB≥0 ⑥
由①⑥解得 q≤
| 16 |
| 9 |
即B所带电荷量的最大值为 Qm=
| 16 |
| 9 |
答:(1)求A在电场中的运动时间t是
|
(2)若B的电荷量q=
| 4 |
| 9 |
| 1 |
| 45 |
(3)为使B离开电场后不改变运动方向,B所带电荷量的最大值qm是
| 16 |
| 9 |

练习册系列答案
相关题目
 如图所示,在xoy平面内,匀强电场的方向沿x轴正向,匀强磁场的方向垂直于xoy平面向里.一电子在xoy平面内运动时,速度方向保持不变.则电子的运动方向沿( )
如图所示,在xoy平面内,匀强电场的方向沿x轴正向,匀强磁场的方向垂直于xoy平面向里.一电子在xoy平面内运动时,速度方向保持不变.则电子的运动方向沿( )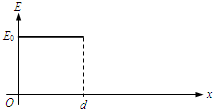 匀强电场的方向沿x轴正向,电场强度E随x的分布如图所示.图中E0和d均为已知量,将带正电的质点A在O点由能止释放,A离开电场足够远后,再将另一带正电的质点B放在O点也由静止释放,当B在电场中运动时,A、B间的相互作用力及相互作用能均为零;B离开电场后,A、B间的相作用视为静电作用,已知A的电荷量为Q,A和B的质量分别为m和
匀强电场的方向沿x轴正向,电场强度E随x的分布如图所示.图中E0和d均为已知量,将带正电的质点A在O点由能止释放,A离开电场足够远后,再将另一带正电的质点B放在O点也由静止释放,当B在电场中运动时,A、B间的相互作用力及相互作用能均为零;B离开电场后,A、B间的相作用视为静电作用,已知A的电荷量为Q,A和B的质量分别为m和 .不计重力.
.不计重力. Q,求两质点相互作用能的最大值Epm;
Q,求两质点相互作用能的最大值Epm;

 .不计重力.
.不计重力. Q,求两质点相互作用能的最大值Epm;
Q,求两质点相互作用能的最大值Epm;