Question

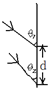（2012?景德镇模拟）如图所示，墙壁上落有两只飞镖，它们是从同一位置水平射出的，飞镖A与竖直墙壁夹角为θ₁，飞镖B与竖直墙壁的夹角为θ₂，两者相距为d，假设飞镖的运动是平抛运动，则射出点到墙壁的水平距离是（　　）

• A．

  2d

  sinθ1-sinθ2

• B．

  2d

  cosθ1-cosθ2

• C．

  2d

  ctgθ2-ctgθ1

• D．

  2d

  tgθ1-tgθ2

Answer 1

分析：两只飞镖水平射出，都做平抛运动，水平方向的分运动是匀速直线运动，竖直方向的分运动是自由落体运动，根据速度的分解，用竖直方向的分速度分别表示出两个飞镖的初速度，由水平距离与初速度之比表示两个飞镖运动的时间、两个飞镖竖直距离之差等于d，即可求解水平距离．

解答：解：设两个飞镖运动的时间分别为t₁和t₂，水平距离为s．
对于飞镖2：初速度大小为：v₀₂=gt₂tanθ₂，运动时间t₂=

s

v02

=

s

gt2tanθ2

，得

t

2 2

=

s

gtanθ2

对于飞镖1：初速度大小为：v₀₁=gt₁tanθ₂，运动时间t₁=

s

v01

=

s

gt1tanθ1

，得

t

2 1

=

s

gtanθ1

又d=

1

2

g

t

2 2

-

1

2

g

t

2 1

联立以上三式得：s=

2d

ctgθ2-ctgθ1

故选C

点评：本题要掌握平抛运动的分解方法：水平方向的分运动是匀速直线运动，竖直方向的分运动是自由落体运动，用竖直方向的分速度表示初速度，用水平距离与初速度之比表示时间是解答的关键．