题目内容
(12分)如图所示,半径分别为R和r的甲、乙两个光滑的圆形轨道安置在同一竖直平面上,轨道之间有一条水平轨道CD相通,一小球以一定的速度先滑上甲轨道,通过动摩擦因数为μ的CD段,又滑上乙轨道,最后离开两圆轨道,若小球在两圆轨道的最高点对轨道的压力都恰好为零,试求CD段的长度.
CD段的长度 。
。
解析试题分析:设小球通过C点时的速度为 ,通过甲轨道最高点的速度为
,通过甲轨道最高点的速度为 ,
,
根据小球对轨道压力为零有 ①(2分)
①(2分)
取轨道最低点所在水平面为参考平面,由机械能守恒定律有 (2分) ②
(2分) ②
联立①②式,可得 (2分)
(2分)
同理可得小球通过D点时的速度 ,(2分)
,(2分)
设CD段的长度为 ,对小球通过CD段的过程,
,对小球通过CD段的过程,
由动能定理有  (2分)
(2分)
解得: (2分)
(2分)
全程列式动能定力也得分。
考点:圆周运动规律的应用,动能定理的应用。

练习册系列答案
相关题目

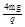 方向竖直向上的匀强电场,在电场内一长为
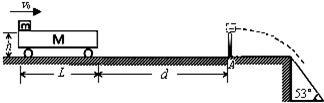
方向竖直向上的匀强电场,在电场内一长为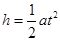 的绝缘细线,一端固定在O点,一端拴着质量m、电荷量q的小球.现将细线拉直到水平位置,使小球由静止释放,当小球运动最高点时细线受到的拉力恰好达到它能承受的最大值而断裂.求:
的绝缘细线,一端固定在O点,一端拴着质量m、电荷量q的小球.现将细线拉直到水平位置,使小球由静止释放,当小球运动最高点时细线受到的拉力恰好达到它能承受的最大值而断裂.求:

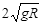 。求:
。求:
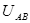 ;
;
 的电场加速后,从C点沿水平方向飞入电场强度为
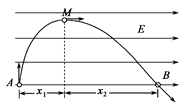
的电场加速后,从C点沿水平方向飞入电场强度为 的匀强电场中,到达该电场中另一点D时,电子的速度方向与电场强度方向的夹角正好是120°,如图所示。试求C、D两点沿电场强度方向的距离y。
的匀强电场中,到达该电场中另一点D时,电子的速度方向与电场强度方向的夹角正好是120°,如图所示。试求C、D两点沿电场强度方向的距离y。