题目内容
 如图所示,A、B两物体(可视为质点)相距s=5m,物体A以VA=4m/s的速度向右匀速直线运动,而物体B此时的速度为VB=8m/s,因摩擦向右做匀减速直线运动,加速度a=-2m/s2.那么物体A追上物体B所用的时间为( )
如图所示,A、B两物体(可视为质点)相距s=5m,物体A以VA=4m/s的速度向右匀速直线运动,而物体B此时的速度为VB=8m/s,因摩擦向右做匀减速直线运动,加速度a=-2m/s2.那么物体A追上物体B所用的时间为( )分析:A作匀速直线运动,B作匀减速直线运动,A追上B时,A的位移比B的位移大5m,在追上之前,最大位移的临界条件出现在A、B速度相等的时候,根据匀变速直线运动的公式进行求解.
解答:解:B做匀减速直线运动,加速度a=-2m/s2,初速度vB=8m/s,当速度减至零时,所用时间为t=
=
s=4s
此过程中B的位移xB=
t=
×4m=16m,
A的位移为xA=vAt=4×4=16m
∵xA<xB+s∴A在B停止运动后才会追上B.
A追上B时A的位移xA′=xB+5m=21m,
所以A追上B的时间t′=
=
s=5.25s
故选A
| 0-vB |
| a |
| 0-8 |
| -2 |
此过程中B的位移xB=
| vB |
| 2 |
| 8 |
| 2 |
A的位移为xA=vAt=4×4=16m
∵xA<xB+s∴A在B停止运动后才会追上B.
A追上B时A的位移xA′=xB+5m=21m,
所以A追上B的时间t′=
| x′A |
| vA |
| 21 |
| 4 |
故选A
点评:A车追上B车位移满足xA=xB+7m.但要注意B车滑行停止后不再运动,需要讨论A车在追上B车之前,B车有无停止.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
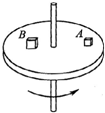 如图所示,A、B两物块置于绕竖直轴匀速转动的水平圆盘上,两物块始终相对圆盘静止,已知两物块的质量mA<mB,运动半径rA>rB,则下列关系一定正确的是( )
如图所示,A、B两物块置于绕竖直轴匀速转动的水平圆盘上,两物块始终相对圆盘静止,已知两物块的质量mA<mB,运动半径rA>rB,则下列关系一定正确的是( )| A、角速度ωA=ωB | B、线速度vA=vB | C、向心加速度aA>aB | D、向心力FA>FB |
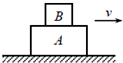 如图所示,A、B两物块叠放在一起,在粗糙的水平面上保持相对静止地向右做匀减速直线运动,运动过程中A受到B对它的摩擦力( )
如图所示,A、B两物块叠放在一起,在粗糙的水平面上保持相对静止地向右做匀减速直线运动,运动过程中A受到B对它的摩擦力( )| A、方向向左,大小不变 | B、方向向左,逐渐减小 | C、方向向右,大小不变 | D、方向向右,逐渐减小 |
 如图所示,A、B两物块质量均为m,用一轻弹簧相连,将A用长度适当的轻绳悬挂于天花板上,系统处于静止状态,B物块恰好与水平桌面接触,此时轻弹簧的伸长量为x,弹簧的弹性势能为Ep,现将悬绳剪断,已知同一弹簧的弹性势能仅与形变量大小有关,且弹簧始终在弹性限度内,则在以后的运动过程中( )
如图所示,A、B两物块质量均为m,用一轻弹簧相连,将A用长度适当的轻绳悬挂于天花板上,系统处于静止状态,B物块恰好与水平桌面接触,此时轻弹簧的伸长量为x,弹簧的弹性势能为Ep,现将悬绳剪断,已知同一弹簧的弹性势能仅与形变量大小有关,且弹簧始终在弹性限度内,则在以后的运动过程中( ) (2011?天津)如图所示,A、B两物块叠放在一起,在粗糙的水平面上保持相对静止地向右做匀减速直线运动,运动过程中B受到的摩擦力( )
(2011?天津)如图所示,A、B两物块叠放在一起,在粗糙的水平面上保持相对静止地向右做匀减速直线运动,运动过程中B受到的摩擦力( ) 如图所示,a、b 两物块质量分别为 m、2m,用不计质量的细绳相连接,悬挂在定滑轮的两侧,不计滑轮质量和一切摩擦.开始时,a、b 两物块距离地面高度相同,用手托住物块 b,然后突然由静止释放,直至 a、b 物块间高度差为 h.在此过程中,下列说法正确的是( )
如图所示,a、b 两物块质量分别为 m、2m,用不计质量的细绳相连接,悬挂在定滑轮的两侧,不计滑轮质量和一切摩擦.开始时,a、b 两物块距离地面高度相同,用手托住物块 b,然后突然由静止释放,直至 a、b 物块间高度差为 h.在此过程中,下列说法正确的是( )