题目内容

物体A做简谐运动的位移xA=4sin（100πt+
π
2
）cm，物体B做简谐运动的位移xB=8sin（100πt+
π
6
）cm．关于A、B的运动，下列说法正确的是（　　）
分析：简谐运动的质点位移的最大值等于振幅．周期是标量，由位移的表达式读出角速度，求出周期．由解析式读出相位差．将t=0.02s代入位移的表达式，再分析位移关系．
解答：解：
A、由两个质点位移的表达式读出：A的振幅为4cm，B的振幅为8cm．故A错误．
B、周期表示质点振动的快慢，没有方向，是标量．由解析式读出两个质点角速度均为T=100πrad/s，周期T=
2π
ω
=0.02s．故B错误．
C、A的相位是100πt+
π
2
，B的相位是100πt+
π
6
，相位差△Φ=（100πt+
π
2
）-（100πt+
π
6
）=
π
3
，所以A的相位始终超前B的相位
π
3
．故C正确．
D、t=0.02s时A、B的位移分别为xA=4sin（100πt+
π
2
）cm=4sin（100π×0.02+
π
2
）cm=4cm，xB=8sin（100πt+
π
6
）cm=8sin（100π×0.02+
π
6
）cm=4cm．则t=0.02s时A、B的位移相等．故D正确．
故选CD
点评：本题知道振动的位移方程，可运用数学知识读出振幅、角速度、相位，能求出任意时刻的位移．
练习册系列答案
相关题目
（2012?马鞍山模拟）Ⅰ．已知用不同的测量工具测量某物体的长度时，有下列不同的结果：
A.2.4cm    B.2.37cm    C.2.372cm    D.2.3721cm
①用最小分度值为毫米的刻度尺测量的结果是
B
B
；
②用有10个等分刻度的游标卡尺测量的结果是
B
B
；
③用螺旋测微器测量的结果是
D
D
．
II．在“利用单摆测重力加速度”的实验中，由单摆做简谐运动的周期公式得到g=
4πlT2
．只要测量出多组单摆的摆长l和运周期T，作出T2-l图象，就可求出当地的重力加速度，理论上T2-l图象是一条过坐标原点的直线．某同学在实验中，用一个直径为d的带孔实心钢球作为摆球，多次改变悬点到摆球顶部的距离l0，分别测出摆球做简谐运动的周期T后，作出T2-1图象，如图1所示．
①造成图象不过坐标原点的原因可能是
A
A

A、将l0记为摆长l；
B、摆球的振幅过小
C、将（lo+d）计为摆长l
D、摆球质量过大
②由图象求出重力加速度g
9.87
9.87
m/s2（取π2=9.87）
Ⅲ．在“描绘小灯泡的伏安特性曲线”的实验中，现除了有一个标有“5V，2.5w”的小灯泡、导线和开关外，还有：
A、直流电源（电动势约为5V，内阻可不计）
B、直流电流表（量程0～3A，内阻约为0.1Ω）
C、直流电流表（量程0～600mA，内阻约为5Ω）
D、直流电压表（量程0～15V，内阻约为15kΩ）
E、直流电压表（量程0～5V，内阻约为10kΩ）
F、滑动变阻器（最大阻值lOΩ，允许通过的最大电流为2A）
G、滑动变阻器（最大阻值lkΩ，允许通过的最大电流为0.5A）
实验要求小灯泡两端的电压从零开始变化并能测多组数据
①实验中电流表应选用
C
C
，电压表应选用
E
E
，滑动变阻器应选用
F
F
（均用序号字母表示）
②某同学通过实验正确地做出了小灯泡的伏安特性曲线如图2甲所示．现把实验中使用的小灯泡接到如图2乙所示的电路中，其中电源电动势为E=6v，内阻r=lΩ，定值电阻R=9Ω，此时灯泡的实际功率为
0.80
0.80
W（结果保留两位有效数字）
选做题（请从A、B和C三小题中选定两小题作答，并在答题卡上把所选题目对应字母后的方框涂满涂黑，如都作答则按A、B两小题评分．）
12A、（选修模块3-3）
（1）下列叙述中正确的是
 

A、一定质量的气体压强越大，则分子的平均动能越大
B、分子间的距离r增大，分子间的作用力做负功，分子势能增大
C、达到热平衡的系统内部各处都具有相同的温度
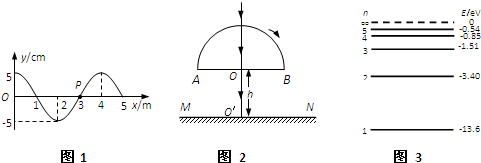
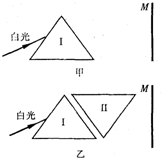D、悬浮在液体中的微粒越大，在某一瞬间撞击它的液体分子数越多，布朗运动越明显精英家教网
（2）若一定质量的理想气体分别按图所示的三种不同过程变化，其中表示等容变化的是
 
（填“a→b“、“b→c“或“c→d′’），该过程中气体
 
（填“吸热”、“放热”或“不吸热也不放热”）．
（3）已知潜水员在岸上和海底吸入空气的密度分别为1.3kg/m3和2.1kg/m3，空气的摩尔质量为0.029kg/mol，阿伏伽德罗常数NA=6.02×1023mol-1．若潜水员呼吸一次吸入2L空气，试估算潜水员在海底比在岸上每呼吸一次多吸入空气的分子数．（结果保留一位有效数字）
B、（选修模块3-4）
（1）下列说法中正确的是
 

A、在光的双缝干涉实验中，若仅将入射光由绿光改为红光，则干涉条纹间距变宽
B、调谐是电磁波发射过程中的一步骤
C、两列水波发生干涉时，如果两列波的波峰在P点相遇，质点P的位移始终最大
D、超声仪器使用超声波而不用普通声波，是因为超声波不易发生衍射
（2）如图甲所示，现有一束白光从图示位置射向棱镜Ι，在足够大的光屏M上形成彩色光谱，下列说法中正确的是
 

精英家教网A、屏M自上而下分布的色光的波长由小到大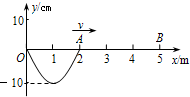
B、在各种色光中，红光通过棱镜时间最长
C、若入射白光绕入射点顺时针旋转，在屏M上最先消失的是紫光
D、若在棱镜Ι和屏M间放置与Ι完全相同的棱镜Ⅱ，相对面平行（如图乙所示），则在屏M上形成的是彩色光谱
（3）如图，质点O在垂直x轴方向上做简谐运动，形成了沿x轴正方向传播的横波．在t=0时刻质点O开始沿Y方向运动，经0.4s第一次形成图示波形，则求该简谐波波速和x=5m处的质点B在t=1.8s时间内通过的路程．
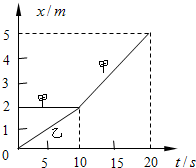
精英家教网
C、（选修模块3-5）
（1）下列四幅图涉及到不同的物理知识，其中说法正确的是
 

精英家教网
A、图甲：普朗克通过研究黑体辐射提出能量子的概念，成为量子力学的奠基人之一
B、图乙：玻尔理论指出氢原子能级是分立的，所以原子发射光子的频率也是不连续的
C、图丙：卢瑟福通过分析α粒子散射实验结果，发现了质子和中子
D、图丁：根据电子束通过铝箔后的衍射图样，可以说明电子具有粒子性
（2）一点光源以功率P向外发出波长为λ的单色光，已知普朗克恒量为h，光速为c，则此光源每秒钟发出的光子数为
 
个，若某种金属逸出功为W，用此光照射某种金属时逸出的光电子的最大初动能为
 
．
（3）在光滑的水平面上有甲、乙两个物体发生正碰，已知甲的质量为1kg，乙的质量为3kg，碰前碰后的位移时间图象如图所示，碰后乙的图象没画，则求碰后乙的速度，并在图上补上碰后乙的图象
精英家教网
（请从A、B和C三小题中选定两小题作答，并在答题卡相应的答题区域内作答，如都作答则按A、B两小题评分．）
A．（选修模块3-3）
（1）下列说法正确的是
 

A．布朗运动是液体分子的无规则运动
B．物体的温度升高时，其分子平均动能增大
C．分子间距离逐渐增大时，分子势能逐渐减小
D．分子间距离增大时，分子间的引力、斥力都减小
（2）空气压缩机在一次压缩过程中，活塞对气缸中的气体做功为2.0×105 J，同时气体放出热量为5.0×104J．在此过程中，该气体的内能
 
（选填“增加”或“减少”）了
 
J．
（3）空调在制冷过程中，室内空气中的水蒸气接触蒸发器（铜管）液化成水，经排水管排走，空气中水份越来越少，人会感觉干燥．某空调工作一段时间后，排出液化水的体积V=1.0×103 cm3．已知水的密度ρ=1.0×103 kg/m3、摩尔质量M=1.8×10-2 kg/mol，阿伏伽德罗常数NA=6.0×1023mol-1．试求：（结果均保留一位有效数字）
①该液化水中含有水分子的总数N=
 
；
②一个水分子的直径d=
 
．
B．（选修模块3-4）
（1）下列说法正确的是
 

A．X射线的频率比无线电波的频率高
B．用同一装置观察光的双缝干涉现象，蓝光的相邻条纹间距比红光的小
C．根据狭义相对论，地面上的人看到高速运行的列车比静止时变短且矮
D．做简谐运动的单摆摆长增大为原来的2倍，其周期也增大为原来的2倍
（2）一列简谐横波在t=0时的波形图如图1所示．介质中
x=3m处的质点P沿y轴方向做简谐运动的表达式
为y=5sin（5πt）cm．则此波沿x轴
 
（选填“正”或“负”）方向传播，传播速度为
 
m/s．
（3）如图2所示，折射率n=
2
的半圆形玻璃砖置于光屏MN的上方，其平面AB到MN的距离为h=10cm．一束单色光沿图示方向射向圆心O，经玻璃砖后射到光屏上的O′点．现使玻璃砖绕圆心O点顺时针转动，光屏上的光点将向哪个方向移动？光点离O′点最远是多少？
 

C．（选修模块3-5）
（1）下列说法正确的是
 

A．光电效应现象揭示了光具有粒子性
B．阴极射线的本质是高频电磁波
C．玻尔提出的原子模型，否定了卢瑟福的原子核式结构学说
D．贝克勒尔发现了天然放射现象，揭示了原子核内部有复杂结构
（2）如图3所示为氢原子的能级示意图．现用能量介于10eV-12.9eV范围内的光子去照射一群处于基态的氢原子，则下列说法正确的是
 

A．照射光中只有一种频率的光子被吸收
B．照射光中有三种频率的光子被吸收
C．氢原子发射出三种不同波长的光
D．氢原子发射出六种不同波长的光
（3）室内装修污染四大有害气体是苯系物、甲醛、氨气和氡．氡存在于建筑水泥、矿渣砖、装饰石材及土壤中．氡看不到，嗅不到，即使在氡浓度很高的环境里，人们对它也毫无感觉．氡进入人的呼吸系统能诱发肺癌，是除吸烟外导致肺癌的第二大因素．静止的氡核86222Rn放出某种粒子x后变成钋核84218Po，粒子x的动能为Ek1，若衰变放出的能量全部变成钋核和粒子x的动能．试回答以下问题：
①写出上述衰变的核反应方程（请用物理学上规定的符号表示粒子x）
 
；
②求钋核的动能Ek2
 
．
精英家教网

（1）对于分子动理论和物体的内能理解，下列说法正确的是
A．液体表面的分子间距较大，所以表现为引力，液体表面有收缩的趋势
B．用力拉铁棒的两端，铁棒没有断，这是分子间存在吸引力的宏观表现
C．理想气体在状态变化时，温度升高，气体分子的平均动能增大，气体的压强也一定增大
D．当分子间的引力和斥力平衡时，分子势能最小
（2）如图所示P-V图，一定质量的理想气体由状态A经过程Ⅰ变至状态B时，从外界吸收热量420J同时膨胀对外做功300J．当气体从状态B经过程Ⅱ回到状态A时，外界压缩气体做功200J，求此过程中气体____________(填“吸收”或“放出”)热量为_________J
（3）某同学在进行“用油膜法估测分子的大小”的实验前，查阅数据手册得知：油酸的摩尔质量M=0.283kg·mol-1，密度ρ=0.895×103kg·m-3.若100滴油酸的体积为1ml，则1滴油酸所能形成的单分子油膜的面积约是多少？(取NA=6.02×1023mol-1.球的体积V与直径D的关系为，结果保留一位有效数字)

12－2．（12分）（供选学3-4模块的考生做）
（1）以下是有关波动和相对论内容的若干叙述，其中正确的有（        ）
A．光速不变原理是：真空中的光速在不同的惯性参考系中都是相同的
B．两列波相叠加产生干涉现象，则振动加强区域与减弱区域交替变化
C．光的偏振现象说明光波是横波
D．夜视仪器能在较冷的背景上探测出较热物体的红外辐射
(2)一束光从空气射向折射率为的某种介质，若反射光线与折射光线垂直，则入射角为__________。真空中的光速为c ，则光在该介质中的传播速度为________________ .
(3)将一劲度系数为K的轻质弹簧竖直悬挂，下端系上质量为m的物块，将物块向下拉离平衡位置后松开，物块上下做简谐运动，其振动周期恰好等于以物块平衡时弹簧的伸长量为摆长的单摆周期．请由单摆周期公式推算出物块做简谐运动的周期T．
Ⅰ．已知用不同的测量工具测量某物体的长度时，有下列不同的结果：
A.2.4cm    B.2.37cm    C.2.372cm    D.2.3721cm
①用最小分度值为毫米的刻度尺测量的结果是    ；
②用有10个等分刻度的游标卡尺测量的结果是    ；
③用螺旋测微器测量的结果是    ．
II．在“利用单摆测重力加速度”的实验中，由单摆做简谐运动的周期公式得到．只要测量出多组单摆的摆长l和运周期T，作出T2-l图象，就可求出当地的重力加速度，理论上T2-l图象是一条过坐标原点的直线．某同学在实验中，用一个直径为d的带孔实心钢球作为摆球，多次改变悬点到摆球顶部的距离l，分别测出摆球做简谐运动的周期T后，作出T2-1图象，如图1所示．
①造成图象不过坐标原点的原因可能是   
A、将l记为摆长l；
B、摆球的振幅过小
C、将（lo+d）计为摆长l
D、摆球质量过大
②由图象求出重力加速度g    m/s2（取π2=9.87）
Ⅲ．在“描绘小灯泡的伏安特性曲线”的实验中，现除了有一个标有“5V，2.5w”的小灯泡、导线和开关外，还有：
A、直流电源（电动势约为5V，内阻可不计）
B、直流电流表（量程0～3A，内阻约为0.1Ω）
C、直流电流表（量程0～600mA，内阻约为5Ω）
D、直流电压表（量程0～15V，内阻约为15kΩ）
E、直流电压表（量程0～5V，内阻约为10kΩ）
F、滑动变阻器（最大阻值lOΩ，允许通过的最大电流为2A）
G、滑动变阻器（最大阻值lkΩ，允许通过的最大电流为0.5A）
实验要求小灯泡两端的电压从零开始变化并能测多组数据
①实验中电流表应选用    ，电压表应选用    ，滑动变阻器应选用    （均用序号字母表示）
②某同学通过实验正确地做出了小灯泡的伏安特性曲线如图2甲所示．现把实验中使用的小灯泡接到如图2乙所示的电路中，其中电源电动势为E=6v，内阻r=lΩ，定值电阻R=9Ω，此时灯泡的实际功率为    W（结果保留两位有效数字）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网