题目内容
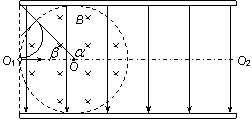
如图所示，带电平行金属板相距为2R，在两板间有垂直纸面向里、磁感应强度为B的圆形匀强磁场区域，与两板及左侧边缘线相切。一个带正电的粒子（不计重力）沿两板间中心线O1O2从左侧边缘O1点以某一速度射入，恰沿直线通过圆形磁场区域，并从极板边缘飞出，在极板间运动时间为t0。若撤去磁场，质子仍从O1点以相同速度射入，则经
时间打到极板上。
（1）求两极板间电压U
（2）若两极板不带电，保持磁场不变，该粒子仍沿中心线O1 O2从O1点射入，欲使粒子从两板左侧间飞出，射入的速度应满足什么条件
解：（1）设粒子从左侧O1点射入的速度为
，极板长为
粒子在初速度方向上做匀速直线运动
，
（2分）
在电场中: 
（1分）
（2分）
（1分）
在复合场中作匀速运动：
（2分）
解得 
（2分）
（2）设粒子在磁场中做圆周运动的轨道半径为r，粒子恰好从上极板左边缘飞出时速度的偏转角为
，由几何关系可知：
，
（2分）
因为 
，所以
（2分）
根据向心力公式 
，解得 r=
（2分）
所以，粒子两板左侧间飞出的条件为 
（2分）
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
）如图13所示，两块平行金属板A、B水平放置，板间距离为d，两金属板分别与电源的正、负极相连接。在距离B板d/2处的O点有一个质量为m的带电液滴恰好保持静止状态，液滴所带电荷为q。
cm。
cm。
v0大小；
cm。
