题目内容
（2012?安徽）如图所示，圆形区域内有垂直于纸面向里的匀强磁场，一个带电粒子以速度v从A点沿直径AOB方向射入磁场，经过△t时间从C点射出磁场，OC与OB成60°角．现将带电粒子的速度变为| v |
| 3 |
分析：由于粒子在匀强磁场是做匀速圆周运动，运动周期 T=
，与粒子速度大小无关，可见，要计算粒子在磁场中运动的时间，只要求得它在磁场中运动轨迹对应的圆心角，就可得到所用的时间．
| 2πm |
| Bq |
解答：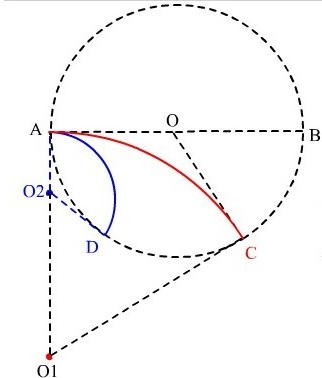
解：设圆形磁场区域的半径是R，
以速度v射入时，半径r1=
，
根据几何关系可知，
=tan60°，所以r1=
R
运动时间t=
T=
T=△t
以速度
射入时，半径r2=
，
所以r2=
=
R
设第二次射入时的圆心角为θ，根据几何关系可知：
tan
=
=
所以θ=120°
则第二次运动的时间为：t=′
=2△t
故选B
解：设圆形磁场区域的半径是R，以速度v射入时，半径r1=
| mv |
| Bq |
根据几何关系可知，
| r1 |
| R |
| 3 |
运动时间t=
| θ |
| 2π |
| 1 |
| 6 |
以速度
| v |
| 3 |
| mv |
| 3Bq |
所以r2=
| r1 |
| 3 |
| ||
| 3 |
设第二次射入时的圆心角为θ，根据几何关系可知：
tan
| θ |
| 2 |
| R |
| r2 |
| 3 |
所以θ=120°
则第二次运动的时间为：t=′
| T |
| 3 |
故选B
点评：带电粒子在磁场中运动的题目解题步骤为：定圆心、画轨迹、求半径，同时还利用圆弧的几何关系来帮助解题．
练习册系列答案
相关题目
（2012?安徽）如图所示，在平面直角坐标系中，有方向平行于坐标平面的匀强电场，其中坐标原点O处的电势为0V，点A处的电势为6V，点B处的电势为3V，则电场强度的大小为（ ）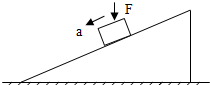
（2012?安徽）如图所示，放在固定斜面上的物块以加速度a沿斜面匀加速下滑，若在物块上再施加一竖直向下的恒力F，则（ ）
（2012?安徽）如图所示，装置的左边是足够长的光滑水平面，一轻质弹簧左端固定，右端连接着质量 M=2kg的小物块A．装置的中间是水平传送带，它与左右两边的台面等高，并能平滑对接．传送带始终以u=2m/s 的速率逆时针转动．装置的右边是一光滑的曲面，质量m=1kg的小物块B从其上距水平台面h=1.0m处由静止释放．已知物块B与传送带之间的摩擦因数μ=0.2，l=1.0m．设物块A、B中间发生的是对心弹性碰撞，第一次碰撞前物块A静止且处于平衡状态．取g=10m/s2．
（2012?安徽）如图所示，在竖直平面内有一个半径为R的圆弧轨道．半径OA水平、OB竖直，一个质量为m的小球自A正上方P点由静止开始自由下落，小球沿轨道到达最高点B时恰好对轨道没有压力，已知AP=2R，重力加速度为g，则小球从P到B的运动过程中（ ）