Question

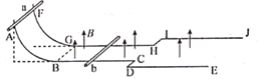
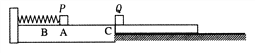
【题目】如图所示，在光滑水平面上静置有质量均为m的木板AB和光滑圆弧滑块CD，其始端D点切线水平且在木板AB上表面内，它们紧靠在一起，一可视为质点的物块P，质量也为m，从木板AB的右端以初速度v0滑上木板AB，过B点时速度为，此后又滑上滑块CD，最终恰好能滑到滑块CD圆弧的最高点C处，已知木板AB上表面粗糙，与物块间的动摩擦因数为μ，求：

（1）物块滑到B处时木板的速度vAB；

（2）木板的最小长度L；

（3）滑块CD圆弧的半径R。

Answer 1

【答案】（1）（2）（3）

【解析】

(1)选向左为正方向，从A到B过程系统动量守恒：

mv0=m+2mvAB

解得：

vAB=

(2)从A到B过程系统能量守恒：

mv02=m+·2mvAB2+μmgL

解得：

L=

(3)从D到C过程，物块P和滑块CD系统水平方向动量守恒：

m+m=2mv共

解得：

v共=

从D到C过程，物块和滑块系统能量守恒：

m+m()2=2mv共2+mgR

解得：

R=