题目内容

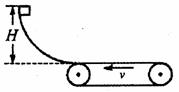
如图所示，质量m＝20kg的物块从光滑曲面上高度H=0.8m处释放，到达底端时水平进入水平传送带，传送带由一电动机驱动着匀速向左转动，速率为3 m/s。已知物块与传送带间的动摩擦因数µ=0.1。 物块冲上传送带后就移走光滑曲面。（g取10m/s2）

（1）若两皮带轮之间的距离是6m，物块将从哪一边离开传送带？

（2）若皮带轮间的距离足够大，从物块滑上到离开传送带的整个过程中，由于物块和传送带间的摩擦而产生了多少热量？

解：（1）设物块在传送带上向右运动的最大距离为S1。

对物块，根据动能定理

mgH-µmgS1=0-0

得：S1=8m>6m     3分

故物块从传送带的右边离开     2分

（2）若皮带轮间的距离足够大，则物块滑上传送带后，将先向右做匀减速运动，再向左做匀加速运动，最后达到与传送带速度相同时做匀速运动离开传送带。

设滑上传送带的速度为υ0，则

，得：υ0=4m/s   

向右匀减速运动过程：时间t1=υ0/µg=4s

此过程中传送带的位移S2=υt1=12m

则相对位移S相1= S1+ S2=20m       4分

同理，可求得向左运动过程中的相对位移S相2=4.5m    2分

故整个过程中因摩擦产生的热量Q=f滑（S相1+ S相2）=490J    2分

练习册系列答案
相关题目

（10分）如图所示，质量m＝2.0×10-3kg的带电小球用绝缘细线竖直地悬挂于电场中，当小球的带电量为q1＝1.0×10-4C时，悬线中的张力为T1＝1.5×10-2N，则小球所在处的场强为多大？当小球的带电量为q2＝－1.0×10-4C时，悬线中的张力T2为多大？

   

如图所示，质量m＝2.0kg的木块静止在高h＝1.8m的水平平台上，木块距平台右边缘d＝7.75m，木块与平台间的动摩擦因数µ＝0.2。用F＝20N的水平拉力拉木块，木块向右运动s1=4.0m时撤去F。不计空气阻力，g取10m/s2。求：

（1）F作用于木块的时间；
（2）木块离开平台时的速度大小；
（3）木块落地时到平台右边缘的水平距离．

(2011年江苏泰州联考)如图所示，质量m＝2.0 kg的物体在水平外力的作用下在水平面上运动，已知物体运动过程中的坐标与时间的关系为，g＝10 m/s2.根据以上条件，求：

(1)t＝10 s时刻物体的位置坐标；
(2)t＝10 s时刻物体的速度和加速度的大小与方向．

如图所示，质量m＝2.0kg的木块静止在高h＝1.8m的水平平台上，木块距平台右边缘d＝7.75m，木块与平台间的动摩擦因数µ＝0.2。用F＝20N的水平拉力拉木块，木块向右运动x1=4.0m时撤去F。不计空气阻力，g取10m/s2。求：

（1）F作用于木块的时间；

（2）木块离开平台时的速度大小；

（3）木块落地时到平台右边缘的水平距离．

 

如图所示，质量m＝2.0kg的木块静止在高h＝1.8m的水平平台上，木块距平台右边缘d＝7.75m，木块与平台间的动摩擦因数µ＝0.2。用F＝20N的水平拉力拉木块，木块向右运动s1=4.0m时撤去F。不计空气阻力，g取10m/s2。求：

（1）F作用于木块的时间；

（2）木块离开平台时的速度大小；

（3）木块落地时到平台右边缘的水平距离．

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网