Question

【题目】在如图所示的xoy平面直角坐标系中，一足够长绝缘薄板正好和x轴的正半轴重合，在全部区域和的条形区域内均分布着方向垂直纸面向里的相同的匀强磁场，且区域磁场上下边界平行。一带正电粒子，从y轴上的（0，a）点以速度v沿与y轴负向成45°角出射。带电粒子与挡板碰撞前后，x方向的分速度不变，y方向的分速度反向、大小不变，且碰撞过程中无电荷量损失。已知粒子质量为m，电荷量为q，磁感应强度的大小，不计粒子的重力。

(1)求粒子进入下方磁场后第一次打在绝缘板上的位置；

(2)为保证粒子不从的下边界射出，磁场下边界位置纵坐标y需要满足的条件；

(3)在满足(2)的情况下，若在绝缘板上的合适位置开一小孔，粒子穿过后能再次回到出发点。写出在板上开这一小孔可能的位置坐标（不需要写出过程）；

(4)在满足(3)的情况下，求粒子从（0，a）出射仅一次经过区域的磁场到再次返回出发点经历的时间。

Answer 1

【答案】(1)击中点的坐标；(2)；(3)（n=0，1，2，3，……）或（n=0，1，2，3，……）；(4) 或

【解析】

(1)粒子的轨迹如图所示，

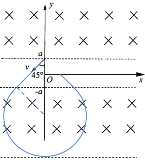
已知由

得

下磁场区域中弦长

所以第一次击中点的坐标

(2)如图，当运动轨迹与磁场下边界相切时，刚好不从y<-a的磁场下边界射出，磁场宽度d应满足：

即磁场下边界位置坐标应满足

(3)开孔位置

（n=0，1，2，3，……）或（n=0，1，2，3，……）

(4)如图，满足题意的运动过程分以下两种情况

若开孔位置在，如甲图所示，所用时间为：

解得

若开孔位置在，如乙图所示，所用时间为：

解得