Question

一个小物块从斜面底端冲上足够长的斜面后又返回到斜面底端，已知小物块的初动能为E，它返回到斜面底端时共克服摩擦力做功为E/2，若小物块以4E的初动能冲上斜面，则返回斜面底端时的动能为___；小物块在前后两次往返过程中所经历的时间之比是___

Answer 1

2E；        1:2

解析考点：功能关系；滑动摩擦力．
分析：选定研究过程，列出动能定理．当物体的动能增加时，加速度不变，物体上升的位移发生改变，找出其中的关系．再次运用动能定理去分析解决问题．
解：以初动能为E运动返回底端过程，应用动能定理得出：W_f1=△E_k1=-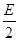
小物块以4E的初动能冲上斜面，加速度不变，速度变为原来的2倍，据v²=2ax得出：上升的位移变为原来的4倍．所以克服摩擦力做的功为-2E．
以初动能为E运动返回底端过程，应用动能定理得出：W_f2=△E_k2=-2E；
则返回斜面底端时的动能为2E．
由于速度变为原来的2倍，根据t=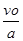得出往返过程中所经历的时间变为原来的两倍．
所以小物块在前后两次往返过程中所经历的时间之比是1：2．
故答案是：2E，1：2．