题目内容
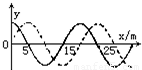
如图所示,实线为t1=0时刻的图象,虚线为t2=0.1s时刻的波形,求:(1)若波的传播方向为+x方向,波速多大;
(2)若波的传播方向为-x方向,波速多大;
(3)若波速为450m/s,波沿什么方向传播.
【答案】分析:(1)若波的传播方向为+x方向,最快传播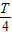 ,根据波的周期性,得到周期的通项式.由题波传播的时间t=0.1s<T,确定特殊值,再由波速公式求解波速.
,根据波的周期性,得到周期的通项式.由题波传播的时间t=0.1s<T,确定特殊值,再由波速公式求解波速.
(2)若波的传播方向为-x方向,最快传播 T,根据波的周期性,得到周期的通项式.由题波传播的时间t=0.1s<T,确定特殊值,再由波速公式求解波速.
T,根据波的周期性,得到周期的通项式.由题波传播的时间t=0.1s<T,确定特殊值,再由波速公式求解波速.
(3)由波速和时间求出波传播的距离,根据波形的平移,确定波的传播方向.
解答:解:
(1)由图线可直接读出波长λ=20m.
若波沿+x方向传播,得t=0.1=(n+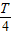 T),周期T为:T=
T),周期T为:T=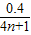 s,(n=0,1,2,…)
s,(n=0,1,2,…)
所以波速为:v=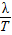 ═50(4n+1)m/s
═50(4n+1)m/s
(2)当波向-x传播时,t=0.1=(n+ )T,(n=0,1,2,…)
)T,(n=0,1,2,…)
得:T=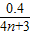 s,
s,
所以波速为:v=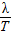 =50(4n+3)m/s
=50(4n+3)m/s
(3)波传播的距离X=vt=450×0.1=45m=2λ+ λ,根据波形的平移法可知波沿+x方向传播.
λ,根据波形的平移法可知波沿+x方向传播.
答:(1)若波的传播方向为+x方向,波速为50(4n+1)m/s,(n=0,1,2,…);
(2)若波的传播方向为-x方向,波速为50(4n+3)m/s,(n=0,1,2,…);
(3)若波速为450m/s,波沿+x方向传播.
点评:本题知道两个时刻的波形,要根据空间的周期性或时间的周期性列出波传播距离或周期的通项式.
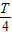 ,根据波的周期性,得到周期的通项式.由题波传播的时间t=0.1s<T,确定特殊值,再由波速公式求解波速.
,根据波的周期性,得到周期的通项式.由题波传播的时间t=0.1s<T,确定特殊值,再由波速公式求解波速.(2)若波的传播方向为-x方向,最快传播
 T,根据波的周期性,得到周期的通项式.由题波传播的时间t=0.1s<T,确定特殊值,再由波速公式求解波速.
T,根据波的周期性,得到周期的通项式.由题波传播的时间t=0.1s<T,确定特殊值,再由波速公式求解波速.(3)由波速和时间求出波传播的距离,根据波形的平移,确定波的传播方向.
解答:解:
(1)由图线可直接读出波长λ=20m.
若波沿+x方向传播,得t=0.1=(n+
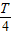 T),周期T为:T=
T),周期T为:T=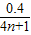 s,(n=0,1,2,…)
s,(n=0,1,2,…)所以波速为:v=
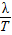 ═50(4n+1)m/s
═50(4n+1)m/s(2)当波向-x传播时,t=0.1=(n+
 )T,(n=0,1,2,…)
)T,(n=0,1,2,…)得:T=
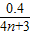 s,
s,所以波速为:v=
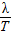 =50(4n+3)m/s
=50(4n+3)m/s(3)波传播的距离X=vt=450×0.1=45m=2λ+
 λ,根据波形的平移法可知波沿+x方向传播.
λ,根据波形的平移法可知波沿+x方向传播.答:(1)若波的传播方向为+x方向,波速为50(4n+1)m/s,(n=0,1,2,…);
(2)若波的传播方向为-x方向,波速为50(4n+3)m/s,(n=0,1,2,…);
(3)若波速为450m/s,波沿+x方向传播.
点评:本题知道两个时刻的波形,要根据空间的周期性或时间的周期性列出波传播距离或周期的通项式.

练习册系列答案
相关题目
 如图所示,实线为t1=0时刻的图象,虚线为t2=0.1s时刻的波形,周期T>0.1s求:
如图所示,实线为t1=0时刻的图象,虚线为t2=0.1s时刻的波形,周期T>0.1s求: 如图所示,实线为t1=0时刻的图象,虚线为t2=0.1s时刻的波形,求:
如图所示,实线为t1=0时刻的图象,虚线为t2=0.1s时刻的波形,求:

