Question

（2002?天津）电视机的显像管中，电子束的偏转是用磁偏转技术实现的．电子束经过电压为U的加速电场后，进入一圆形匀强磁场区，如图所示．磁场方向垂直于圆面．磁场区的圆心为O，半径为r．当不加磁场时，电子束将通过O点打到屏幕的中心M点，为了让电子束射到屏幕边缘的P点，需要加磁场，使电子束偏转一已知角度θ，此时磁场的磁感应强度B为多少？

Answer 1

分析：电子在电场运动时，电场力做正功，根据动能定理求出电子进入磁场时的速度．电子在磁场中由洛伦兹力提供向心力，做匀速圆周运动，电子束偏转角度θ，则电子运动轨迹的圆心角也为θ，根据几何知识求出轨迹半径R，再由牛顿第二定律求出B．

解答：解：电子在磁场中沿圆孤ab运动，圆心为c，半径为R，v表示电子进入磁场时的速度，m、e分别表示电子的质量和电量，如图所示．则：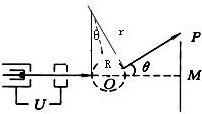
根据动能定理得   eU=

1

2

mv²    ①
又由牛顿第二定律得  Bev=m

v2

R

 ②
   tan

θ

2

=

r

R

                  ③
解以上各式可得：B=

1

r

2mU e

tan

θ

2

答：磁场的磁感应强度B为

1

r

2mU e

tan

θ

2

．

点评：带电粒子在电磁场中运动问题，可以按照力学的方法分析受力情况和运动情况．在磁场中运动时，关键是利用几何知识画轨迹、求半径．