题目内容
如图所示，两带电平行板A、B间的电场为匀强电场，场强E=8.0×102V/m，两板间距d=16cm，板长L=30cm．一带电量q=1.0×10-16C、质量m=1.0×10-24kg的粒子以v=3×105m/s的速度沿平行于板方向从两板的正中间射入电场后向着B板偏转，不计带电粒子的重力，求：（1）粒子待何种电荷？在电场中运动时间为多久？
（2）粒子废除电场时的偏转角的正弦值为多大．
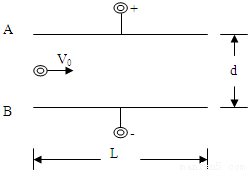
【答案】分析：（1）电场方向向下，粒子向下偏转，电场力向下，说明粒子带正电．粒子在平行于板的方向做匀速直线运动，由板长和初速度求出运动的时间．
（2）将速度分解为水平方向和竖直方向，根据牛顿第二定律求出加速度，由vy=at求出竖直方向分速度，再求解偏转角的正弦值
解答：解：（1）粒子带正电．粒子在水平方向做匀速直线运动，
则粒子在电场中运动时间t=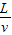
=
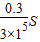=1×10-6S
（2）粒子的加速度a=
vy=at=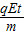
设粒子飞出除电场时偏转角为θ
则tanθ=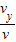
=
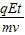≈0.27
答：（1）粒子带正电．粒子在电场中运动时间为1×10-6S．
（2）粒子飞出电场时的偏转角的正弦值为0.27．
点评：本题考查运用力学规律处理电场问题的能力，比较容易．对于类平抛运动常常采用运动的合成与分解方法处理，分解为平行于电场的匀加速直线运动和垂直于电场的匀速直线运动．
（2）将速度分解为水平方向和竖直方向，根据牛顿第二定律求出加速度，由vy=at求出竖直方向分速度，再求解偏转角的正弦值
解答：解：（1）粒子带正电．粒子在水平方向做匀速直线运动，
则粒子在电场中运动时间t=
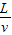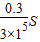==1×10-6S（2）粒子的加速度a=
vy=at=
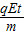
设粒子飞出除电场时偏转角为θ
则tanθ=
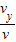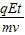=≈0.27答：（1）粒子带正电．粒子在电场中运动时间为1×10-6S．
（2）粒子飞出电场时的偏转角的正弦值为0.27．
点评：本题考查运用力学规律处理电场问题的能力，比较容易．对于类平抛运动常常采用运动的合成与分解方法处理，分解为平行于电场的匀加速直线运动和垂直于电场的匀速直线运动．
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
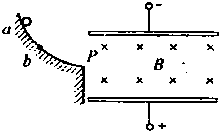
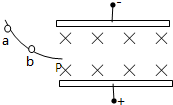如图所示，两带电平行金属板水平放置，板间匀强磁场方向垂直纸面向里，某带电小球从光滑绝缘轨道上的a点自由滑下，经过轨道端点P进入板间后恰能沿水平方向作直线运动．现使小球从较低的b点开始下滑，经P点进入板间，则在两板间的运动过程中（ ）
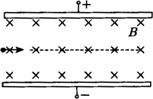
如图所示，两带电平行金属板A、B间的电场为匀强电场，场强E=4.0×102V/m，两板相距d=16cm，板长L=30cm．一带电量q=1.0×10-16C、质量m=1.0×10-22㎏的粒子沿平行于板方向从两板的正中间射入电场后向着B板偏转，不计带电粒子所受重力，（tan28°=0.53）求：
如图所示，两带电平行金属板A、B间的电场为匀强电场，场强E=4.0×102V/m，两板相距d=16cm，板长L=30cm．一带电量q=1.0×10-16C、质量m=1.0×10-22㎏的粒子沿平行于板方向从两板的正中间射入电场后向着B板偏转，不计带电粒子所受重力，（tan28°=0.53）求：