题目内容
 质量为m的滑块与竖直墙面间动摩擦因数为μ,力F1水平向左作用在滑块上,滑块从静止开始竖直向下做匀加速运动,如图所示.若再施加另一个方向与竖直方向成α角的恒力F2(图中未画出),发现滑块的加速度大小和方向恰好保持不变.则下列结论正确的是( )
质量为m的滑块与竖直墙面间动摩擦因数为μ,力F1水平向左作用在滑块上,滑块从静止开始竖直向下做匀加速运动,如图所示.若再施加另一个方向与竖直方向成α角的恒力F2(图中未画出),发现滑块的加速度大小和方向恰好保持不变.则下列结论正确的是( )分析:分推力F2斜向左上、斜向左下、斜向右上、斜向右下四种情况,根据牛顿第二定律列式分析即可.
解答:解:没有加推力F2前,物体受推力F1、重力、支持力和滑动摩擦力,根据牛顿第二定律,有:
mg-μF1=ma ①
加推力F2后,假设推力斜向左下,根据牛顿第二定律,有:
mg+F2cosα-μ(F2sinα+F1)=ma ②
加推力F2后,假设推力斜向左上,根据牛顿第二定律,有:
mg-F2cosα-μ(F2sinα+F1)=ma ③
加推力F2后,假设推力斜向右下,根据牛顿第二定律,有:
mg+F2cosα-μ(-F2sinα+F1)=ma ④
加推力F2后,假设推力斜向右上,根据牛顿第二定律,有:
mg-F2cosα-μ(-F2sinα+F1)=ma ⑤
由①②解得:μ=cotα;
由①③联立,无解;
由①④解得:无解;
由①⑤解得:μ=cotα;
故μ=cotα;
故A正确,BCD错误;
故选A.
mg-μF1=ma ①
加推力F2后,假设推力斜向左下,根据牛顿第二定律,有:
mg+F2cosα-μ(F2sinα+F1)=ma ②
加推力F2后,假设推力斜向左上,根据牛顿第二定律,有:
mg-F2cosα-μ(F2sinα+F1)=ma ③
加推力F2后,假设推力斜向右下,根据牛顿第二定律,有:
mg+F2cosα-μ(-F2sinα+F1)=ma ④
加推力F2后,假设推力斜向右上,根据牛顿第二定律,有:
mg-F2cosα-μ(-F2sinα+F1)=ma ⑤
由①②解得:μ=cotα;
由①③联立,无解;
由①④解得:无解;
由①⑤解得:μ=cotα;
故μ=cotα;
故A正确,BCD错误;
故选A.
点评:本题关键分4种情况,然后根据牛顿第二定律列式分析,较难.

练习册系列答案
相关题目
 [物理--一选修3-5]
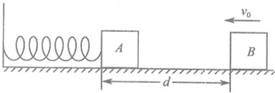
[物理--一选修3-5] 质量为m的滑块与竖直墙面间动摩擦因数为μ,力F1水平向左作用在滑块上,滑块从静止开始竖直向下做匀加速运动,如图所示.若再施加另一个方向与竖直方向成α角的恒力F2(图中未画出),发现滑块的加速度大小和方向恰好保持不变.则下列结论正确的是
质量为m的滑块与竖直墙面间动摩擦因数为μ,力F1水平向左作用在滑块上,滑块从静止开始竖直向下做匀加速运动,如图所示.若再施加另一个方向与竖直方向成α角的恒力F2(图中未画出),发现滑块的加速度大小和方向恰好保持不变.则下列结论正确的是
