题目内容
如图所示,一对平行光滑轨道放置在水平面上,两轨道间距L=0.20m,电阻R=8Ω,有一电阻r=2Ω,质量m=1kg的金属棒ab垂直平放在轨道上,轨道电阻可忽略不计,整个装置处于垂直轨道平面向下的匀强磁场中,磁感应强度B=5T,现用一外力F沿轨道方向拉金属棒,使之做初速为零的匀加速直线运动,加速度a=1m/s2.试求:(1)2s内通过电阻R的电量Q大小;
(2)外力F与时间t的关系;
(3)求当t=5s时电阻R上的电功率PR和F的功率PF的大小,并用能量守恒的观点说明两者为何不相等?

【答案】分析:(1)金属棒做初速为零的匀加速直线运动,由运动学公式位移求出2s通过的位移,由Q=I△t、I= 、E=
、E= 结合求解电量Q;
结合求解电量Q;
(2)推导出安培力的表达式,根据牛顿第二定律得到外力F与时间t的关系式;
(3)当t=5s时,求出感应电流,即可求出电阻R上的电功率PR,PF=Fv.分析能量如何转化来解释:外力F的功率转化为用于导体棒动能增加的机械功率和电阻上的发热功率,而发热功率还包括电阻R上的功率和导体棒电阻r的功率,所以有PR<PF.
解答:解:(1)t=2s时,金属棒通过的位移为 x=
回路磁通量的变化量为△Φ=BxL=2Wb
感应电流为
则电量
代入解得 Q=0.2C
(2)安培力表达式为FA=BIL=B L=
L=
代入解得,
根据牛顿第二定律得 F-FA=ma
则得 F=1+0.1t
(3)当t=5s时, ,
,
则PR=I2R=2W,
因F=1.5N,v=at=5m/s,则PF=Fv=7.5W.
外力F的功率转化为用于导体棒动能增加的机械功率和电阻上的发热功率,而发热功率还包括电阻R上的功率和导体棒电阻r的功率,所以有PR<PF.
答:(1)2s内通过电阻R的电量Q大小是0.2C;
(2)外力F与时间t的关系是F=1+0.1t;
(3)当t=5s时电阻R上的电功率PR是2W,F的功率PF的大小是7.5W,外力F的功率转化为用于导体棒动能增加的机械功率和电阻上的发热功率,而发热功率还包括电阻R上的功率和导体棒电阻r的功率,所以有PR<PF.
点评:本题中用到两个经验公式:一是感应电荷量公式q= ;二是安培力公式FA=
;二是安培力公式FA= .对于能量问题,关键要分析能量有几种形式,把握能量是如何转化的.
.对于能量问题,关键要分析能量有几种形式,把握能量是如何转化的.
 、E=
、E= 结合求解电量Q;
结合求解电量Q;(2)推导出安培力的表达式,根据牛顿第二定律得到外力F与时间t的关系式;
(3)当t=5s时,求出感应电流,即可求出电阻R上的电功率PR,PF=Fv.分析能量如何转化来解释:外力F的功率转化为用于导体棒动能增加的机械功率和电阻上的发热功率,而发热功率还包括电阻R上的功率和导体棒电阻r的功率,所以有PR<PF.
解答:解:(1)t=2s时,金属棒通过的位移为 x=

回路磁通量的变化量为△Φ=BxL=2Wb
感应电流为

则电量

代入解得 Q=0.2C
(2)安培力表达式为FA=BIL=B
 L=
L=
代入解得,

根据牛顿第二定律得 F-FA=ma
则得 F=1+0.1t
(3)当t=5s时,
 ,
,则PR=I2R=2W,
因F=1.5N,v=at=5m/s,则PF=Fv=7.5W.
外力F的功率转化为用于导体棒动能增加的机械功率和电阻上的发热功率,而发热功率还包括电阻R上的功率和导体棒电阻r的功率,所以有PR<PF.
答:(1)2s内通过电阻R的电量Q大小是0.2C;
(2)外力F与时间t的关系是F=1+0.1t;
(3)当t=5s时电阻R上的电功率PR是2W,F的功率PF的大小是7.5W,外力F的功率转化为用于导体棒动能增加的机械功率和电阻上的发热功率,而发热功率还包括电阻R上的功率和导体棒电阻r的功率,所以有PR<PF.
点评:本题中用到两个经验公式:一是感应电荷量公式q=
 ;二是安培力公式FA=
;二是安培力公式FA= .对于能量问题,关键要分析能量有几种形式,把握能量是如何转化的.
.对于能量问题,关键要分析能量有几种形式,把握能量是如何转化的. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目









 注入人体,
注入人体,
 D.液体表面层的分子比液体内部的分子有更大的分子势能
D.液体表面层的分子比液体内部的分子有更大的分子势能 D.超声波可以在真空中传播
D.超声波可以在真空中传播
 注入人体,
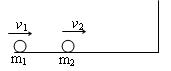
注入人体, ⑶如图所示,质量分别为m1和m2的两个小球在光滑水平面上分别以速度v1、v2同向运动,并发生对心碰撞,碰后m2被右侧墙壁原速弹回,又与m1碰撞,再一次碰撞后两球都静止.求第一次碰后m1球速度的大小.
⑶如图所示,质量分别为m1和m2的两个小球在光滑水平面上分别以速度v1、v2同向运动,并发生对心碰撞,碰后m2被右侧墙壁原速弹回,又与m1碰撞,再一次碰撞后两球都静止.求第一次碰后m1球速度的大小.