题目内容
11. 由不同介质制成的两个半径均为R的透明四分之一圆柱体Ⅰ和Ⅱ紧靠在一起,截面如图所示,圆心为O,顶部交点为D,以O为原点建立直角坐标系xoy.红色光束1从介质Ⅰ底部的A(-$\frac{\sqrt{3}}{2}$R,0)点垂直于界面入射;红色光束2平行于y轴向下射入介质Ⅱ,入射点为B且∠BOD=60°.已知透明介质Ⅰ对红光的折射率n1=$\sqrt{2}$,透明介质Ⅱ对红光的折射率n2=$\sqrt{3}$.求:光束1经过柱面反射或折射后与y轴交点和光束2经柱体下底面折射后与y轴交点之间的距离.
由不同介质制成的两个半径均为R的透明四分之一圆柱体Ⅰ和Ⅱ紧靠在一起,截面如图所示,圆心为O,顶部交点为D,以O为原点建立直角坐标系xoy.红色光束1从介质Ⅰ底部的A(-$\frac{\sqrt{3}}{2}$R,0)点垂直于界面入射;红色光束2平行于y轴向下射入介质Ⅱ,入射点为B且∠BOD=60°.已知透明介质Ⅰ对红光的折射率n1=$\sqrt{2}$,透明介质Ⅱ对红光的折射率n2=$\sqrt{3}$.求:光束1经过柱面反射或折射后与y轴交点和光束2经柱体下底面折射后与y轴交点之间的距离.
分析 红光线1通过玻璃砖后不偏折.射到圆弧面上时根据入射角与临界角的大小,判断可知发生了全反射.光线2在圆柱面上的入射角为60°,根据折射定律求出折射角,由几何知识求出在底面上的入射角,再由折射定律求出折射角,作出光路图.根据几何关系求解即可.
解答 解:红光线1对介质 I的全反射临界角为:C1=arcsin$\frac{1}{{n}_{1}}$=arcsin$\frac{1}{\sqrt{2}}$=45°
而光线1由A点入射后的入射角 i1=60°>45°,所以将会发生全反射,反射后恰好交y轴于D点(如图所示).
设红光线2在B点发生的折射的折射角为r2,由折射定律n2=$\frac{sin{i}_{2}}{sin{r}_{2}}$得:
sinr2=$\frac{sin{i}_{2}}{{n}_{2}}$=$\frac{1}{2}$
所以:r2=30°
光线2再传播到底部介面时入射角 i3=30°
光线2对介质Ⅱ的全反射临界角为:C2=arcsin$\frac{1}{{n}_{2}}$$\frac{\frac{1}{2}R}{cos30°}$=60°,所以不会发生全反射.
再由折射定律得:r3=60°
设光线2射出后交y轴于P点:OP=$\frac{\frac{1}{2}R}{cos30°}$•tan30°=$\frac{1}{3}$R
所以所求的距离 d=DP=R+$\frac{1}{3}$R=$\frac{4}{3}$R
答:光束1经过柱面反射或折射后与y轴交点和光束2经柱体下底面折射后与y轴交点之间的距离为$\frac{4}{3}$R.
点评 本题的关键是掌握全反射的条件:光从光密介质射入光疏介质,入射角大于临界角,能正确作出光路图,运用几何知识辅助分析.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
6. 图甲所示的“轨道康复者”航天器可在太空中给“垃圾”卫星补充能源,延长卫星的使用寿命.图乙是“轨道康复者”在某次拯救一颗地球同步卫星前,二者在同一平面内沿相同绕行方向绕地球做匀速圆周运动的示意图,此时二者的连线通过地心、轨道半径之比为1:4.若不考虑卫星与“轨道康复者”之间的引力,则下列说法正确的是( )
图甲所示的“轨道康复者”航天器可在太空中给“垃圾”卫星补充能源,延长卫星的使用寿命.图乙是“轨道康复者”在某次拯救一颗地球同步卫星前,二者在同一平面内沿相同绕行方向绕地球做匀速圆周运动的示意图,此时二者的连线通过地心、轨道半径之比为1:4.若不考虑卫星与“轨道康复者”之间的引力,则下列说法正确的是( )
 图甲所示的“轨道康复者”航天器可在太空中给“垃圾”卫星补充能源,延长卫星的使用寿命.图乙是“轨道康复者”在某次拯救一颗地球同步卫星前,二者在同一平面内沿相同绕行方向绕地球做匀速圆周运动的示意图,此时二者的连线通过地心、轨道半径之比为1:4.若不考虑卫星与“轨道康复者”之间的引力,则下列说法正确的是( )
图甲所示的“轨道康复者”航天器可在太空中给“垃圾”卫星补充能源,延长卫星的使用寿命.图乙是“轨道康复者”在某次拯救一颗地球同步卫星前,二者在同一平面内沿相同绕行方向绕地球做匀速圆周运动的示意图,此时二者的连线通过地心、轨道半径之比为1:4.若不考虑卫星与“轨道康复者”之间的引力,则下列说法正确的是( )| A. | 在图示轨道上,“轨道康复者”的速度小于7.9km/s | |
| B. | 在图示轨道上,“轨道康复者”的加速度大小是地球同步卫星的4倍 | |
| C. | 在图示轨道上,“轨道康复者”的周期为3h,且从图示位置开始经1.5h与同步卫星的距离最近 | |
| D. | 若要对该同步卫星实施拯救,“轨道康复者”应从图示轨道上加速,然后与同步卫星对接 |
16.1971年7月26号发射的阿波罗-15号飞船首次把一辆月球车送上月球,美国宇航员斯特做了一个落体实验:在月球上的同一高度同时释放羽毛和铁锤,下列说法正确的是(月球上是真空)( )
| A. | 羽毛先落地,铁锤后落地 | |
| B. | 铁锤先落地,羽毛后落地 | |
| C. | 铁锤和羽毛运动的加速度都等于物体在地球上的重力加速度g | |
| D. | 铁锤和羽毛同时落地,运动的加速度相同但不等于物体在地球上的重力加速度g |
3.关于电场强度E的说法正确的是( )
| A. | 电场中某点的电场强度方向跟正电荷在该点所受到的电场力的方向相同 | |
| B. | 电场中某点的电场强度方向跟负电荷在该点所受到的电场力的方向相同 | |
| C. | 根据E=$\frac{F}{q}$可知,电场中某点的电场强度与电场力F成正比,与电量q成反比 | |
| D. | 一个正电荷激发的电场的电场强度处处相同,是一个匀强电场 |
20. 如图所示,实线是某电场中的电场线,A、B两处分别放置电量为Q1、Q2的正带电试探电荷且Q1>Q2.以下有关A、B两处的比较不正确的是( )
如图所示,实线是某电场中的电场线,A、B两处分别放置电量为Q1、Q2的正带电试探电荷且Q1>Q2.以下有关A、B两处的比较不正确的是( )
 如图所示,实线是某电场中的电场线,A、B两处分别放置电量为Q1、Q2的正带电试探电荷且Q1>Q2.以下有关A、B两处的比较不正确的是( )
如图所示,实线是某电场中的电场线,A、B两处分别放置电量为Q1、Q2的正带电试探电荷且Q1>Q2.以下有关A、B两处的比较不正确的是( )| A. | A处的场强较大 | |
| B. | A处的电势较高 | |
| C. | 带电粒子Q1在A处受到的电场力较大 | |
| D. | 带电粒子Q1在A处的电势能一定较大 |
1. 一定质量的理想气体经历了如图所示的ab、bc、cd、da四个过程,其中bc的延长线通过原点,cd垂直于ab且与T轴平行,da与bc平行,则气体体积( )
一定质量的理想气体经历了如图所示的ab、bc、cd、da四个过程,其中bc的延长线通过原点,cd垂直于ab且与T轴平行,da与bc平行,则气体体积( )
 一定质量的理想气体经历了如图所示的ab、bc、cd、da四个过程,其中bc的延长线通过原点,cd垂直于ab且与T轴平行,da与bc平行,则气体体积( )
一定质量的理想气体经历了如图所示的ab、bc、cd、da四个过程,其中bc的延长线通过原点,cd垂直于ab且与T轴平行,da与bc平行,则气体体积( )| A. | 在ab过程中不断增大 | B. | 在bc过程中保持不变 | ||
| C. | 在cd过程中不断增大 | D. | 在da过程中保持不变 |
 如图所示,在x轴上方存在沿x轴正方向场强为E的匀强电场,在x轴下方的矩形区域ABCD内存在垂直于纸面向外的匀强磁场,矩形区域的AB边与x轴重合,M点是y轴上的一点,在M点有一质量为m、电荷量为e的质子,以初速度v0沿y轴负方向开始运动,恰好从N点进入磁场,当质子第二次经过x轴时电场反向,质子恰好回到M点,若|OM|=2|ON|,不计质子的重力.求:
如图所示,在x轴上方存在沿x轴正方向场强为E的匀强电场,在x轴下方的矩形区域ABCD内存在垂直于纸面向外的匀强磁场,矩形区域的AB边与x轴重合,M点是y轴上的一点,在M点有一质量为m、电荷量为e的质子,以初速度v0沿y轴负方向开始运动,恰好从N点进入磁场,当质子第二次经过x轴时电场反向,质子恰好回到M点,若|OM|=2|ON|,不计质子的重力.求: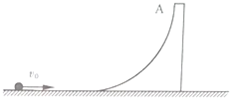 如图所示,质量M=2kg,半径R=0.3m的四分之一竖直光滑圆弧槽,静置在光滑水平面上,槽的末端和水平面相切,一质量m=1kg,可视为质点的光滑小球,以初速度v0冲上圆弧槽,g=10m/s2,求:
如图所示,质量M=2kg,半径R=0.3m的四分之一竖直光滑圆弧槽,静置在光滑水平面上,槽的末端和水平面相切,一质量m=1kg,可视为质点的光滑小球,以初速度v0冲上圆弧槽,g=10m/s2,求: