��Ŀ����
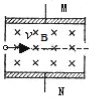
����Ŀ����ͼ��ʾΪ��ֱ���ڵ�ֱ������ϵxOy��A�������Ϊ��-8 m��0����C�������Ϊ��-4 m��O����A���Ҳ���������������y�����������ǿ�糡��-4 m>x��-8m����ij�ǿ��СΪE1=5 V��m��0>x��-4 m����ij�ǿ��СΪE2=7 V��m��x��O����ij�ǿ��СΪE3 =5V/m;��һ���������ڵĴų������෴�Ҵ�ֱ������ƽ�棬�Ÿ�Ӧǿ�ȴ�С��ΪB=2 T������һ�������С���A����z����������vo=4 m/s�����ʽ���糡����֪С�������m =2��10-3 kg�������q =4��10-3 C������糡�ʹų������㹻���㣬С�����Ϊ�ʵ��ҵ�������ֲ��䣬����С�����˶��еĵ�ŷ��䣬�������ٶ�ȡg=10 m��s2����

(1)С��y��ʱ���ٶȣ�
(2)С���A���˶�������Ϊ(56 m��y)�ĵ㾭����ʱ�䡣
���𰸡���1��4![]() m/s 450��2����2+
m/s 450��2����2+![]() ��s��2+
��s��2+![]() ��s��2+
��s��2+![]() ��s
��s
��������(1)��![]() ����С�����ܵ糡��
����С�����ܵ糡��![]()
�������ݵã� ![]()
����֪�� ![]()
�� ![]()
����С��������ֱ���˶�����ù��̾���ʱ��Ϊt1
��![]() ����
���� ![]() ��С������ƽ���˶�����ù��̾���ʱ��Ϊt2�������˶�ѧ����
��С������ƽ���˶�����ù��̾���ʱ��Ϊt2�������˶�ѧ����
��y�������� ![]()
�������ݵã� ![]()
![]()
![]()
��x�������� ![]()
�������ݵã� ![]() ��
�� ![]() ��
�� ![]()
�ɣ� ![]()
�������ݽ�ã� ![]()
��v��y��������ļн�Ϊ![]()
�ɣ� ![]()
�������ݽ�ã� ![]()
(2)��![]() ����
���� ![]() ������֪��С�����ڵ�һ�������뾶Ϊr������Ϊ
������֪��С�����ڵ�һ�������뾶Ϊr������Ϊ![]() ������Բ���˶������Ž����ڵ��ġ���һ�������뾶Ϊr������Ϊ
������Բ���˶������Ž����ڵ��ġ���һ�������뾶Ϊr������Ϊ![]() ������Բ���˶����켣��ͼ��ʾ��
������Բ���˶����켣��ͼ��ʾ��

���������ṩ���������У� ![]()
�������ݵã� ![]()
��С���ڵ�һ����һ�ε���x���λ��ΪP�㣬�ڶ��ε���x���λ��ΪG��
�ɼ��ι�ϵ�ã� ![]() ��
�� ![]()
С��������Բ���˶�������Ϊ�� ![]()
�������ݵã� ![]()
��С���O�㵽��x����H(56m��0)���ʱ��Ϊt3
�� ![]() ����
����![]()
�ʣ� ![]()
�������ݵã� ![]()
�֣� ![]()
�ﵽ������Ϊ56m�ĵ����������������
(i)���������Ϊ56m��I�㣬 ![]()
(ii)���������Ϊ56m��H�㣬 ![]()
(iii)���������Ϊ56m��J�㣬 ![]()