题目内容
（12分）如图所示，在足够大倾角为θ的光滑斜面上，有一长为l的细线，细线的一端固定在O点，另一端拴一质量为m的小球，现使小球恰好能在斜面上做完整的圆周运动，已知O点到斜面底边的距离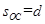
，求：
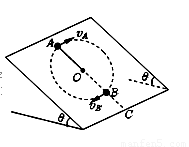
（1）小球通过最高点A时的速度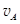
；
（2）小球通过最低点B时，细线对小球的拉力；
（3）小球运动到A点或B点时细线断裂，小球滑落到斜面底边时与C点的距离若相等，则l和d应满足什么关系？
【答案】
（1）
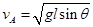（2）
（3）
【解析】
试题分析：(1)小球在斜面上通过圆周运动最高点时，受重力支持力和拉力而且重力和斜面支持力和合力沿斜面向下大小等于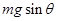
，使小球恰好能在斜面上做完整的圆周运动即最高点时拉力等于0，所以
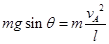计算得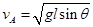
（2）从A点到B点，根据动能定理有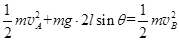
，计算得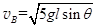
，最低点的拉力假设为T，则有
，计算得
（3）不管从A点绳子断裂还是从B点绳子断裂，小球的运动都是类平抛运动，加速度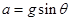
细线在A点断裂：
细线在B点断裂：
又
联立解得：
考点：圆周运动 平抛运动
练习册系列答案
相关题目
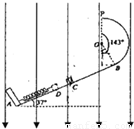
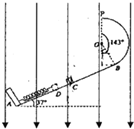如图所示，AB为倾龟θ=37°的绝缘直轨道，轨道的AC部分光滑，CB部分粗糙．BP为半径R=1.0m的绝缘竖直光滑圆弧形轨道，O为圆心，圆心角∠BOP=143°、两轨道相切于B点，P、O两点在同一竖直线上．轻弹簧下端固定在A点上端自由伸展到C点，整个装置处在竖直向下的足够大的匀强电场中，场强E=1.0×106N/C．现有一质量m=2.0kg、带负电且电量大小恒为q=1.0×10-5C的物块（视为质点），靠在弹簧上端（不拴接），现用外力推动物块，使弹簧缓慢压缩到D点，然后迅速撤去外力，物块被反弹到C点时的速度VC=10m/So物块与轨道CB间的动摩擦因素μ=0.50，C、D间的距离L=1．Om5物块第一次经过B点后恰能到P点．（sin37°=0.6，cos37°=0.8，g 取 10m/s2） 