题目内容
质量为60kg的消防队员从一根固定的竖直金属杆上由静止滑下，经2.5s落地．消防队员受到的竖直向上的摩擦力变化情况如图所示，取g=10m/s2．在消防队员下滑的过程中：（1）他向下加速与减速的加速度大小分别多大？
（2）他落地时的速度多大？
（3）他克服摩擦力做的功是多少？
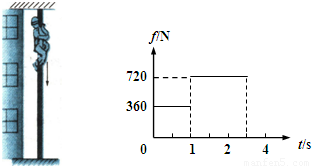
【答案】分析：（1）根据消防队员受到的摩擦力与重力的关系，分析消防队员的运动情况，由牛顿第二定律求解加速度．
（2）由运动学速度公式求出他落地时的速度．
（3）根据位移公式求出他下滑的高度，再求解他克服摩擦力做的功．
解答：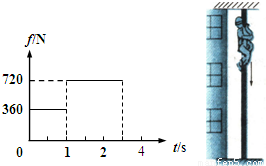
解：（1）消防队员的重力G=mg=600N，则该队员先在t1=1s的时间内以加速度a1匀加速下滑，然后在t2=1.5s的时间内以加速度a2匀减速下滑．
在第1s内，由牛顿第二定律，得：
mg-f1=ma1
得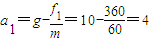
（m/s2）
后1.5s内由牛顿第二定律得：
f2-mg=ma2
得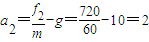
（m/s2）
（2）他在1s末时的速度为
vm=a1t1=4×1=4m/s
落地时的速度
vt=vm-a2t2=4-2×1.5=1m/s
（3）该队员在第1s内下滑的高度
h1=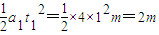
在后1.5 s内下滑的高度
h1=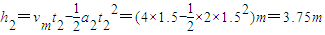
他克服摩擦力做的功为W=f1h1+f2h2=（360×2+720×3.75）J=3420J
答：
（1）他向下加速与减速的加速度大小分别为4m/s2和2m/s2．
（2）他落地时的速度为1m/s．
（3）他克服摩擦力做的功是3420J．
点评：本题有两个过程，运用牛顿定律和运动学公式结合求解是基本的方法，也可以运用动量定理和动能定理结合处理．
（2）由运动学速度公式求出他落地时的速度．
（3）根据位移公式求出他下滑的高度，再求解他克服摩擦力做的功．
解答：
解：（1）消防队员的重力G=mg=600N，则该队员先在t1=1s的时间内以加速度a1匀加速下滑，然后在t2=1.5s的时间内以加速度a2匀减速下滑．在第1s内，由牛顿第二定律，得：
mg-f1=ma1
得
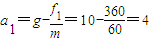（m/s2）后1.5s内由牛顿第二定律得：
f2-mg=ma2
得
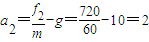（m/s2）（2）他在1s末时的速度为
vm=a1t1=4×1=4m/s
落地时的速度
vt=vm-a2t2=4-2×1.5=1m/s
（3）该队员在第1s内下滑的高度
h1=
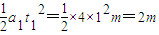
在后1.5 s内下滑的高度
h1=
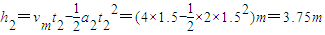
他克服摩擦力做的功为W=f1h1+f2h2=（360×2+720×3.75）J=3420J
答：
（1）他向下加速与减速的加速度大小分别为4m/s2和2m/s2．
（2）他落地时的速度为1m/s．
（3）他克服摩擦力做的功是3420J．
点评：本题有两个过程，运用牛顿定律和运动学公式结合求解是基本的方法，也可以运用动量定理和动能定理结合处理．
练习册系列答案
相关题目
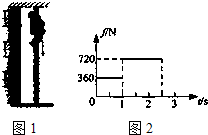如图1所示，质量为60kg的消防队员从一根固定的竖直金属杆上由静止滑下，经过2.5s时间落到地面上．下滑中消防队员受到的竖直向上的摩擦力随时间变化的情况如图2所示，取g=10m/s2．求：
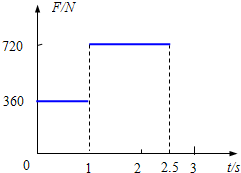（2010?渭南一模）质量为60kg的消防队员，从一根竖直的长直轻绳上由静止滑下，经2.5s落地．轻绳上端有一力传感器，它记录的轻绳受到的拉力变化情况如图甲所地，取g=10m/s2．下列说法中正确的是（ ）
如图所示，长为12m的钢管沿着竖直方向固定在地面上．一名质量为60kg的消防队员在演习训练中，从钢管顶端由静止开始先匀加速再匀减速下滑，滑到地面时速度恰好为零．如果他加速时的加速度大小是减速时的2倍，下滑的总时间为3s，g 取10m/s2．关于消防队员在下滑的过程中，下列说法正确的是（ ）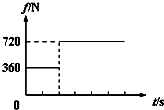
质量为60kg的消防队员从一根固定的、高度为6m的竖直金属杆顶端由静止滑下，消防队员受到的竖直向上的摩擦力变化情况如图所示（消防员视为质点）．在消防队员下滑的过程中：