题目内容
如图(a),小球甲固定于水平气垫导轨的左端,质量m=0.4kg的小球乙可在导轨上无摩擦地滑动,甲、乙两球之间因受到相互作用而具有一定的势能,相互作用力沿二者连线且随间距的变化而变化.现已测出势能随位置x的变化规律如图(b)中的实线所示.已知曲线最低点的横坐标x=20cm,虚线①为势能变化曲线的渐近线,虚线②为经过曲线上某点的切线.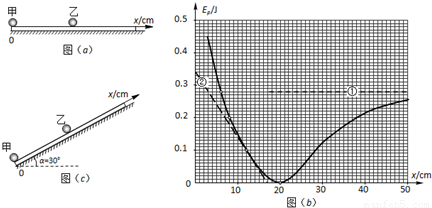
(1)将小球乙从x1=8cm处由静止释放,小球乙所能达到的最大速度为多大?
(2)假定导轨右侧足够长,将小球乙在导轨上从何处由静止释放,小球乙不可能第二次经过x=20cm的位置?并写出必要的推断说明;
(3)若将导轨右端抬高,使其与水平面的夹角α=30°,如图(c)所示.将球乙从x2=6cm处由静止释放,小球乙运动到何处时速度最大?并求其最大速度;
(4)在图(b)上画出第(3)问中小球乙的动能Ek与位置x的关系图线.
【答案】分析:(1)根据功能关系可知,当势能最小时,动能最大,速度最大.
(2)根据题意正确进行受力分析,明确小球的运动形式,根据能量守恒可正确解答.
(3)由图得出释放时的势能便是整个运动过程中的总能量,根据能量转化与守恒可知势能最小时动能最大,据此可求得最大速度和最大位移.
(4)图象是关于图线 III与图线 II对称的曲线.
解答:解:(1)球乙运动到x=20cm位置时势能最小,速度最大,由能量守恒可得:
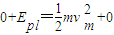
解出: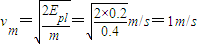
答:小球乙所能达到的最大速度为1m/s.
(2)在0<x<6cm区间内将小球乙由静止释放,不可能第二次经过x.
原因:在0<x<6cm区间内两球之间的作用力为排斥力,在20cm<x<∞区间内两球之间作用力为吸引力,无穷远处和6cm处的势能为0.28J.若小球乙的静止释放点在6cm<x<∞区间,小球乙做往复运动,多次经过x=20cm的位置.而静止释放点在0<x<6cm区间内时,初态势能大于0.28J,小球乙将会到无穷远处而无法返回,只能经过x位置一次.
(3)x3=12cm处的切线斜率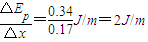 ,
,
表明此处乙球受到甲球2N的排斥力,乙球此处受到重力的分力为mgsinα=2N.
所以,乙球在x3=12cm处时,所受合外力等于零,速度最大.
从图中读出x3=12cm处的势能EP3=0.1J,x2=6cm处的势能Ep2=0.28J,
能量守恒: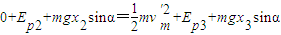
解出: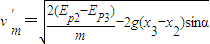 =
=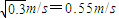
答:小球乙运动到x3=12cm时速度最大,其最大速度为0.55m/s.
(4)得出图象如下所示,注意几个特殊位置,x2=6cm处的动能为Ek=0;x3=12cm处的动能Ek=0.06J,x4=20cm处的动能Ek=0J.
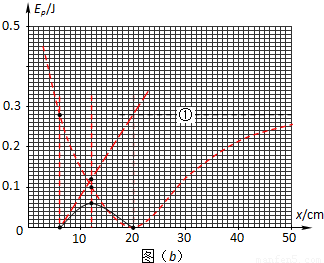
点评:本题考查包括重力势能和动能在内的能量守恒,还要读图和作图,有一定难度,难点在,此类题在高考中很少出现过,是创新.是考查学生能力的好题.
(2)根据题意正确进行受力分析,明确小球的运动形式,根据能量守恒可正确解答.
(3)由图得出释放时的势能便是整个运动过程中的总能量,根据能量转化与守恒可知势能最小时动能最大,据此可求得最大速度和最大位移.
(4)图象是关于图线 III与图线 II对称的曲线.
解答:解:(1)球乙运动到x=20cm位置时势能最小,速度最大,由能量守恒可得:
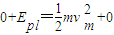
解出:
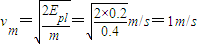
答:小球乙所能达到的最大速度为1m/s.
(2)在0<x<6cm区间内将小球乙由静止释放,不可能第二次经过x.
原因:在0<x<6cm区间内两球之间的作用力为排斥力,在20cm<x<∞区间内两球之间作用力为吸引力,无穷远处和6cm处的势能为0.28J.若小球乙的静止释放点在6cm<x<∞区间,小球乙做往复运动,多次经过x=20cm的位置.而静止释放点在0<x<6cm区间内时,初态势能大于0.28J,小球乙将会到无穷远处而无法返回,只能经过x位置一次.
(3)x3=12cm处的切线斜率
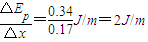 ,
,表明此处乙球受到甲球2N的排斥力,乙球此处受到重力的分力为mgsinα=2N.
所以,乙球在x3=12cm处时,所受合外力等于零,速度最大.
从图中读出x3=12cm处的势能EP3=0.1J,x2=6cm处的势能Ep2=0.28J,
能量守恒:
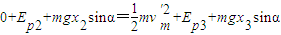
解出:
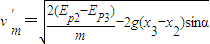 =
=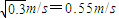
答:小球乙运动到x3=12cm时速度最大,其最大速度为0.55m/s.
(4)得出图象如下所示,注意几个特殊位置,x2=6cm处的动能为Ek=0;x3=12cm处的动能Ek=0.06J,x4=20cm处的动能Ek=0J.

点评:本题考查包括重力势能和动能在内的能量守恒,还要读图和作图,有一定难度,难点在,此类题在高考中很少出现过,是创新.是考查学生能力的好题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目