Question

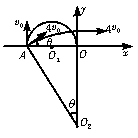
如图所示，坐标平面第Ⅰ象限内存在大小为E，方向向左的匀强电场，第Ⅱ象限内存在大小为B，方向垂直纸面向里的匀强磁场，足够长的挡板MN垂直x轴放置且距原点O为D．一质量为m，电量为-q的粒子(不计重力)，若从距原点O为一定距离的A点，以大小为v₀，方向垂直x轴向上的速度进入磁场，则粒子恰好到达O点而不进入电场．现该粒子仍从A点进入磁场，但初速度大小为4v₀，为使粒子进入电场后能垂直打到挡板MN上，求：

(1)粒子在A点进入磁场时，速度方向与x轴正向的夹角．

(2)粒子打到挡板上时，速度的大小．

 

Answer 1

答案：
解析：

设计意图：本题考查了带电粒子在匀强磁场中的匀速圆周运动及在匀强电场中的匀加速直线运动，同时也考查了学生的分析与综合能力及运用数学工具解决物理问题的能力． 解析：(1)当粒子以速度v0垂直进入匀强磁场区域时，在洛伦兹力的作用下，以O1为圆心做匀速圆周运动，恰好能过坐标原点O而不进入电场．据洛伦兹力提供向心力，有 qv0B=m 解得r= 据几何关系可知，r=． 当粒子以4v0从同一点垂直进入匀强磁场区域时，在洛伦兹力的作用下，以O2为圆心做匀速圆周运动，为使粒子进入电场后能垂直打在MN上，进入电场的速度方向应水平向右．在这种情况下，圆周的半径为 R==4r=2OA． 由几何关系可知，q =30°． 即粒子速度的方向与x轴正向的夹角为30°，如上图所示． (2)粒子水平向右进入电场中后，在电场力的作用下做匀加速直线运动，据动能定理，得 qEd=m(4v0)2 解得粒子打到挡板上时，速度的大小为 v= 易错点：求解第(2)问时，将4v0误认为v0，导致解题错误． 答案：(1)q =30°　(2)v=

提示：