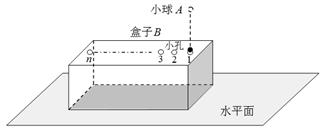
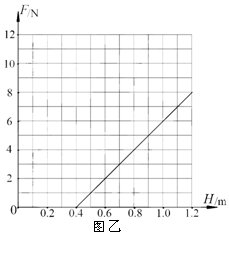
题目内容
(1)摩擦力对物块做的功为4.5J;(2)小物块对轨道的压力大小为60N;倾斜挡板与水平面的夹角为θ为60°。
解析试题分析: 设小物块经过C点时的速度大小 ,因为经过C时恰好能完成圆周运动,由牛顿第二定律可得:
,因为经过C时恰好能完成圆周运动,由牛顿第二定律可得: ;解得
;解得 =3m/s;
=3m/s;
小物块由A到B过程中,设摩擦力对小物块做的功为W,由动能定理得: ,解得W=4.5J
,解得W=4.5J
故摩擦力对物块做的功为4.5J.
设小物块经过D点时的速度为 ,对由C点到D点的过程,由动能定理的:
,对由C点到D点的过程,由动能定理的:
小物块经过D点时,设轨道对它的支持力大小为 ,由牛顿第二定律得:
,由牛顿第二定律得:
联立解得 =60N,
=60N, =3
=3 m/s
m/s
由牛顿第三定律可知,小物块对轨道的压力大小为60N
小物块离开D点做平抛运动,设经时间t打在E点,由
设小物块打在E点时速度的水平、竖直分量分别为 ,
,
 =
=
 =gt
=gt
又tanα= =
=
联立解得α=60°
再由几何关系可得θ=α=60°
故倾斜挡板与水平面的夹角为θ为60°.
考点:动能定理的应用;牛顿第二定律;向心力;机械能守恒定律

练习册系列答案
相关题目

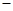 。现用质量m0=0.4kg的小物块a将弹簧缓慢压缩到C点,释放后弹簧恢复原长时物块恰停止在B点。用同种材料、质量为m=0.2kg、带+q的绝缘小物块b将弹簧缓慢压缩到C点,释放后,小物块b离开桌面由M点沿半圆轨道运动,恰好能通过轨道的最高点P。(取g= 10m/s2)求:
。现用质量m0=0.4kg的小物块a将弹簧缓慢压缩到C点,释放后弹簧恢复原长时物块恰停止在B点。用同种材料、质量为m=0.2kg、带+q的绝缘小物块b将弹簧缓慢压缩到C点,释放后,小物块b离开桌面由M点沿半圆轨道运动,恰好能通过轨道的最高点P。(取g= 10m/s2)求:

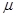 )。某时刻观察到细线偏离竖直方向
)。某时刻观察到细线偏离竖直方向 角,
角,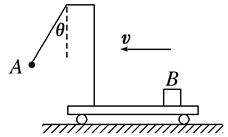


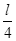 、质量为m的小球用两根不可伸长的轻绳a、b连接,两轻绳的另一端系在一根竖直杆的A、B两点上,A、 B两点相距为l,当两轻绳伸直后,A、B两点到球心的距离均为l。当竖直杆以自己为轴转动并达到稳定时(细绳a、b与杆在同一竖直平面内)。求:
、质量为m的小球用两根不可伸长的轻绳a、b连接,两轻绳的另一端系在一根竖直杆的A、B两点上,A、 B两点相距为l,当两轻绳伸直后,A、B两点到球心的距离均为l。当竖直杆以自己为轴转动并达到稳定时(细绳a、b与杆在同一竖直平面内)。求: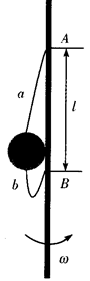
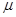 =0.2.盒内存在着某种力场,每当小球进入盒内,该力场将同时对小球和盒子施加一个大小为F=Mg、方向分别竖直向上和向下的恒力作用;每当小球离开盒子,该力F同时立即消失.盒子的上表面开有一系列略大于小球的小孔,孔间距满足一定的关系,使得小球进出盒子的过程中始终不与盒子接触.当小球A以v=1m/s的速度从孔1进入盒子的瞬间,盒子B恰以v0=6m/s的速度向右滑行.取重力加速度g=10m/s2,小球恰能顺次从各个小孔进出盒子.试求:
=0.2.盒内存在着某种力场,每当小球进入盒内,该力场将同时对小球和盒子施加一个大小为F=Mg、方向分别竖直向上和向下的恒力作用;每当小球离开盒子,该力F同时立即消失.盒子的上表面开有一系列略大于小球的小孔,孔间距满足一定的关系,使得小球进出盒子的过程中始终不与盒子接触.当小球A以v=1m/s的速度从孔1进入盒子的瞬间,盒子B恰以v0=6m/s的速度向右滑行.取重力加速度g=10m/s2,小球恰能顺次从各个小孔进出盒子.试求: