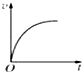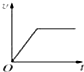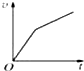题目内容
 传送带与水平面夹角为θ=37°,其上、下两端点AB间的距离是26.6m,BC为一光滑的水平平台(物体从传送带传送到BC平台上时的速度大小不变),CDEF是一深井,已知CD高度为5m,DE长4m,传送带在电动机的带动下,以4.Om/s的速度顺时针匀速运转,现将质量为lkg 的物体(可视为质点)无初速度的轻放于传送带的A点,已知物体与传送带间的动摩擦因数为μ=0.8,重力加速度 g=10m/s2,sin37°=0.6,cos37°=0.80)
传送带与水平面夹角为θ=37°,其上、下两端点AB间的距离是26.6m,BC为一光滑的水平平台(物体从传送带传送到BC平台上时的速度大小不变),CDEF是一深井,已知CD高度为5m,DE长4m,传送带在电动机的带动下,以4.Om/s的速度顺时针匀速运转,现将质量为lkg 的物体(可视为质点)无初速度的轻放于传送带的A点,已知物体与传送带间的动摩擦因数为μ=0.8,重力加速度 g=10m/s2,sin37°=0.6,cos37°=0.80)(1)在传送带将物体从A点传送到B点过程中,求物体刚放上传送带时的加速度大小;
(2)若传送带因故障被卡住,现对物体从A点开始提供水平拉力F=64.375N,求拉力至少需要作用多长时间,使物体从C点水平抛出后刚好可以落到井底的E端.(设物体落到井底DK时没有弹起)
分析:以物体为研究对象,受力分析利用牛顿第二定律求解;物体在拉力的作用下先加速,撤掉拉力做减速运动,在光滑平台匀速运动,最后做平抛运动,利用牛顿运动定律即可求解.
解答:解:(1)对物体进行受力分析,由牛顿第二定律可得:μmgcosθ-mgsinθ=ma
代入数据解之得:a=0.4m/s2
(2)物体在传送带AB上加速时的加速度大小为a1,时间为t1,减速时的加速度大小为a2,时间为t2;物体到达B点时速度为vB,物体从C点抛出时速度为vC,且有vB=vC,落到地板DE时所用时间为t3.
C到E的过程中,物体做平抛运动,所以:
hCD=
g
…①
xDE=vCt3…②
联立①②解得:vC=4m/s…③
A到B的过程中:Fcosθ-μ(mgcosθ+Fsinθ)-mgsinθ=ma1…④
μmgcosθ+mgsinθ=ma2…⑤
由运动学公式得:
a1
+
t2=xAB…⑥
vB=a1t1-a2t2…⑦
联立②③④⑤⑥⑦代入数据解得:t1=2s
答:(1)在传送带将物体从A点传送到B点过程中,求物体刚放上传送带时的加速度大小为 0.4m/s2;
(2)若传送带因故障被卡住,现对物体从A点开始提供水平拉力F=64.375N,求拉力至少需要作用2s,使物体从C点水平抛出后刚好可以落到井底的E端.
代入数据解之得:a=0.4m/s2
(2)物体在传送带AB上加速时的加速度大小为a1,时间为t1,减速时的加速度大小为a2,时间为t2;物体到达B点时速度为vB,物体从C点抛出时速度为vC,且有vB=vC,落到地板DE时所用时间为t3.
C到E的过程中,物体做平抛运动,所以:
hCD=
| 1 |
| 2 |
| t | 2 3 |
xDE=vCt3…②
联立①②解得:vC=4m/s…③
A到B的过程中:Fcosθ-μ(mgcosθ+Fsinθ)-mgsinθ=ma1…④
μmgcosθ+mgsinθ=ma2…⑤
由运动学公式得:
| 1 |
| 2 |
| t | 2 1 |
| a1t1+vB |
| 2 |
vB=a1t1-a2t2…⑦
联立②③④⑤⑥⑦代入数据解得:t1=2s
答:(1)在传送带将物体从A点传送到B点过程中,求物体刚放上传送带时的加速度大小为 0.4m/s2;
(2)若传送带因故障被卡住,现对物体从A点开始提供水平拉力F=64.375N,求拉力至少需要作用2s,使物体从C点水平抛出后刚好可以落到井底的E端.
点评:解本题的关键正确对物体受力分析,判断对应的运动情况,灵活应用牛顿运动定律列方程求解;注意多过程中,速度是联系前后运动的纽带.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
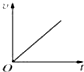
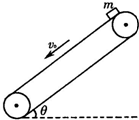 (2008?潍坊模拟)如图所示,足够长的传送带与水平面夹角为θ,以速度v0逆时针匀速转动.在传送带的上端轻轻放置一个质量为m的小木块,小木块与传送带间的动摩擦因数μ<tanθ,则下图中能客观地反映小木块的1,3,5速度随时间变化关系的是( )
(2008?潍坊模拟)如图所示,足够长的传送带与水平面夹角为θ,以速度v0逆时针匀速转动.在传送带的上端轻轻放置一个质量为m的小木块,小木块与传送带间的动摩擦因数μ<tanθ,则下图中能客观地反映小木块的1,3,5速度随时间变化关系的是( ) 在工厂的流水线上安装有传送带,用传送带传送工件,可大大提高工作效率.如图所示,传送带与水平面夹角为θ=30°,其上、下两端点A、B间的距离是3.84m.传送带在电动机的带动下,以4.0m/s顺时针匀速运转.现将质量为10kg的工件(可视为质点)轻放于传送带的A点,已知工件与传送带间的动摩擦因数为
在工厂的流水线上安装有传送带,用传送带传送工件,可大大提高工作效率.如图所示,传送带与水平面夹角为θ=30°,其上、下两端点A、B间的距离是3.84m.传送带在电动机的带动下,以4.0m/s顺时针匀速运转.现将质量为10kg的工件(可视为质点)轻放于传送带的A点,已知工件与传送带间的动摩擦因数为 如图所示,足够长的传送带与水平面夹角为θ=37°,以速度v0=10m/s逆时针匀速转动.在传送带的上端轻轻放置一个质量为m的小木块,AB长度是20m,小木块与传送带间的动摩擦因数μ=0.5,则下列说法正确的是( )
如图所示,足够长的传送带与水平面夹角为θ=37°,以速度v0=10m/s逆时针匀速转动.在传送带的上端轻轻放置一个质量为m的小木块,AB长度是20m,小木块与传送带间的动摩擦因数μ=0.5,则下列说法正确的是( )