题目内容
某校举行托乒乓球跑步比赛,赛道为水平直道,比赛距离为s.比赛时.某同学将球置于球拍中心,以大小为a的加速度从静止开始做匀加速直线运动,当速度达到v时,再以v做匀速直线运动跑至终点.整个过程中球一直保持在球拍中心不动.比赛中,该同学在匀速直线运动阶段保持球拍的倾角为θ,如图所示,设球在运动中受到的空气阻力大小与其速度大小成正比,方向与运动方向相反,不计球与球拍之间的摩擦,球的质量为m,重力加速度为g.(1)求空气阻力大小与球速大小的比例系数k;
(2)求在加速跑阶段球拍倾角θ随速度v变化的关系式;
(3)整个匀速跑阶段,若该同学速度仍为v,而球拍的倾角比θ大了β并保持不变,不计球在球拍上的移动引起的空气阻力变化,为保证到达终点前球不从球拍上距离中心为r的下边沿掉落,求β应满足的条件.

【答案】分析:(1)在匀速运动阶段,受力平衡,根据平衡条件列式即可求解;
(2)加速阶段,设球拍对球的支持力为N′,根据牛顿第二定律即可求解;
(3)根据牛顿第二定律求出球沿球拍面下滑的加速度,当球运动的位移小于等于r时,球不从球拍上掉落,根据运动学基本公式列式即可求解.
解答:解:(1)在匀速运动阶段,有mgtanθ=kv
得k=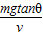
(2)加速阶段,设球拍对球的支持力为N′,有
N′sinθ-kv=ma
N′cosθ=mg
得tanθ=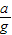 +
+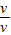 tanθ
tanθ
(3)以速度v匀速运动时,设空气阻力与重力的合力为F,有F=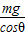
球拍倾角为θ+β时,空气阻力与重力的合力不变,设球沿球拍面下滑的加速度大小为a′,有
Fsinβ=ma′
设匀速跑阶段所用时间为t,有t=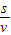 -
-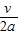
球不从球拍上掉落的条件 a′t2≤r
a′t2≤r
得sinβ≤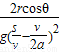
答:(1)空气阻力大小与球速大小的比例系数k为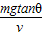 ;
;
(2)在加速跑阶段球拍倾角θ随速度v变化的关系式为tanθ=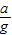 +
+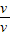 tanθ;
tanθ;
(3)β应满足的条件为sinβ≤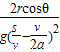 .
.
点评:本题主要考查了牛顿第二定律及运动学基本公式的应用,要求同学们能正确受力分析,难度适中.
(2)加速阶段,设球拍对球的支持力为N′,根据牛顿第二定律即可求解;
(3)根据牛顿第二定律求出球沿球拍面下滑的加速度,当球运动的位移小于等于r时,球不从球拍上掉落,根据运动学基本公式列式即可求解.
解答:解:(1)在匀速运动阶段,有mgtanθ=kv
得k=
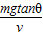
(2)加速阶段,设球拍对球的支持力为N′,有
N′sinθ-kv=ma
N′cosθ=mg
得tanθ=
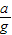 +
+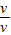 tanθ
tanθ(3)以速度v匀速运动时,设空气阻力与重力的合力为F,有F=
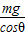
球拍倾角为θ+β时,空气阻力与重力的合力不变,设球沿球拍面下滑的加速度大小为a′,有
Fsinβ=ma′
设匀速跑阶段所用时间为t,有t=
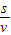 -
-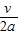
球不从球拍上掉落的条件
 a′t2≤r
a′t2≤r得sinβ≤
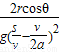
答:(1)空气阻力大小与球速大小的比例系数k为
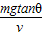 ;
;(2)在加速跑阶段球拍倾角θ随速度v变化的关系式为tanθ=
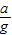 +
+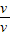 tanθ;
tanθ;(3)β应满足的条件为sinβ≤
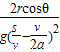 .
.点评:本题主要考查了牛顿第二定律及运动学基本公式的应用,要求同学们能正确受力分析,难度适中.

练习册系列答案
相关题目
 某校举行托乒乓球跑步比赛,赛道为水平直道,比赛时某同学将球置于球拍中心,当速度达到v0时做匀速直线运动跑至终点,整个过程中球一直保持在球拍中心不动,如图所示.设球在运动中受到的空气阻力大小与其速度大小成正比,f=kv0,方向与运动方向相反,不计球与球拍之间的摩擦,球的质量为m,重力加速度为g.则在比赛中,该同学在匀速直线运动阶段保持球拍的倾角θ0满足( )
某校举行托乒乓球跑步比赛,赛道为水平直道,比赛时某同学将球置于球拍中心,当速度达到v0时做匀速直线运动跑至终点,整个过程中球一直保持在球拍中心不动,如图所示.设球在运动中受到的空气阻力大小与其速度大小成正比,f=kv0,方向与运动方向相反,不计球与球拍之间的摩擦,球的质量为m,重力加速度为g.则在比赛中,该同学在匀速直线运动阶段保持球拍的倾角θ0满足( )A、sinθ0=
| ||
B、cosθ0=
| ||
C、tanθ0=
| ||
D、tanθ0=
|
 (2012?重庆)某校举行托乒乓球跑步比赛,赛道为水平直道,比赛距离为s.比赛时.某同学将球置于球拍中心,以大小为a的加速度从静止开始做匀加速直线运动,当速度达到v0时,再以v0做匀速直线运动跑至终点.整个过程中球一直保持在球拍中心不动.比赛中,该同学在匀速直线运动阶段保持球拍的倾角为θ0,如图所示,设球在运动中受到的空气阻力大小与其速度大小成正比,方向与运动方向相反,不计球与球拍之间的摩擦,球的质量为m,重力加速度为g.
(2012?重庆)某校举行托乒乓球跑步比赛,赛道为水平直道,比赛距离为s.比赛时.某同学将球置于球拍中心,以大小为a的加速度从静止开始做匀加速直线运动,当速度达到v0时,再以v0做匀速直线运动跑至终点.整个过程中球一直保持在球拍中心不动.比赛中,该同学在匀速直线运动阶段保持球拍的倾角为θ0,如图所示,设球在运动中受到的空气阻力大小与其速度大小成正比,方向与运动方向相反,不计球与球拍之间的摩擦,球的质量为m,重力加速度为g.
 ;
; 随速度
随速度 变化的关系式;
变化的关系式;
