题目内容
如图4所示,长度为l的细绳上端固定在天花板上O点,下端拴着质量为m的小球。当把细绳拉直时,细绳与竖直线夹角为θ=60°,此时小球静止于光滑的水平面上。

(1)当球以角速度 做圆锥摆运动时,细绳的张力T为多大?水平面受到的压力N是多大?
做圆锥摆运动时,细绳的张力T为多大?水平面受到的压力N是多大?
(2)当球以角速度 做圆锥摆运动时,细绳的张力
做圆锥摆运动时,细绳的张力 及水平面受到的压力
及水平面受到的压力 各是多大?
各是多大?

(1)当球以角速度
 做圆锥摆运动时,细绳的张力T为多大?水平面受到的压力N是多大?
做圆锥摆运动时,细绳的张力T为多大?水平面受到的压力N是多大?(2)当球以角速度
 做圆锥摆运动时,细绳的张力
做圆锥摆运动时,细绳的张力 及水平面受到的压力
及水平面受到的压力 各是多大?
各是多大? (1) ,
, (2)
(2) ,
,
 ,
, (2)
(2) ,
,
设小球做圆锥摆运动的角速度为 时,小球对光滑水平面的压力恰好为零,此时球受重力mg和绳的拉力T0,应用正交分解法则列出方程:
时,小球对光滑水平面的压力恰好为零,此时球受重力mg和绳的拉力T0,应用正交分解法则列出方程:
 ①
①
 ②
②
由以上二式解得: ③
③
(1)∵ ,所以小球受重力mg,绳的拉力T和水平面的支持力N,应用正交分解法列方程:
,所以小球受重力mg,绳的拉力T和水平面的支持力N,应用正交分解法列方程: ④
④
 ⑤
⑤
解得: ,
,
(2)∵ ,小球离开水平面做圆锥摆运动,设细绳与竖直线的夹角为
,小球离开水平面做圆锥摆运动,设细绳与竖直线的夹角为 ,小球受重力mg和细绳的拉力
,小球受重力mg和细绳的拉力 ,应用正交分解法列方程:
,应用正交分解法列方程:
 ⑥
⑥
 ⑦(2分)
⑦(2分)
解得: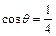 ,
, ,
,
由于球已离开水平面,所以球对水平面的压力 。
。
 时,小球对光滑水平面的压力恰好为零,此时球受重力mg和绳的拉力T0,应用正交分解法则列出方程:
时,小球对光滑水平面的压力恰好为零,此时球受重力mg和绳的拉力T0,应用正交分解法则列出方程: ①
①  ②
②由以上二式解得:
 ③
③(1)∵
 ,所以小球受重力mg,绳的拉力T和水平面的支持力N,应用正交分解法列方程:
,所以小球受重力mg,绳的拉力T和水平面的支持力N,应用正交分解法列方程: ④
④  ⑤
⑤解得:
 ,
,
(2)∵
 ,小球离开水平面做圆锥摆运动,设细绳与竖直线的夹角为
,小球离开水平面做圆锥摆运动,设细绳与竖直线的夹角为 ,小球受重力mg和细绳的拉力
,小球受重力mg和细绳的拉力 ,应用正交分解法列方程:
,应用正交分解法列方程: ⑥
⑥  ⑦(2分)
⑦(2分)解得:
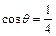 ,
, ,
,由于球已离开水平面,所以球对水平面的压力
 。
。
练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目




