题目内容
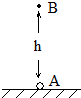
 如图所示,在A点固定一正电荷,电量为Q,在离A高度为H的C处由静止释放某带同种电荷的液珠,开始运动瞬间的加速度大小恰好为重力加速度g.已知静电常量为k,两电荷均可看成点电荷,不计空气阻力.求:
如图所示,在A点固定一正电荷,电量为Q,在离A高度为H的C处由静止释放某带同种电荷的液珠,开始运动瞬间的加速度大小恰好为重力加速度g.已知静电常量为k,两电荷均可看成点电荷,不计空气阻力.求:(1)液珠的比荷
(2)液珠速度最大时离A点的距离h.
(3)若已知在点电荷Q的电场中,某点的电势可表示成?=
| kQ | r |
分析:(1)根据牛顿第二定律,通过瞬间的加速度求出液珠的比荷.
(2)当液珠加速度为零时,速度最大,根据重力和库仑力平衡求出液珠速度最大时离A点的距离.
(3)根据动能定理,通过最高点速度为零,求出液珠能到达的最高点B离A点的高度.
(2)当液珠加速度为零时,速度最大,根据重力和库仑力平衡求出液珠速度最大时离A点的距离.
(3)根据动能定理,通过最高点速度为零,求出液珠能到达的最高点B离A点的高度.
解答:解(1)设液珠的电量为q,质量为m,由题意知,当液珠在C点时k
-mg=mg
比荷为
=
(2)当液珠速度最大时k
=mg
得 h=
H
(3)设BC间的电势差大小UCB,由题意得
UCB=?C-?B=
-
对由释放至液珠到达最高点(速度为零)的全过程应用动能定理得qUCB-mg(rB-H)=0
即q(
-
)-mg(rB-H)=0
将第(1)问的结果代入化简 rB2-3HrB+2H2=0
解得rB=2H rB′=H(舍去)
答:(1)液珠的比荷为
=
.
(2)液珠速度最大时离A点的距离h=
H.
(3)液珠能到达的最高点B离A点的高度为2H.
| H2 |
比荷为
| q |
| m |
| 2gH2 |
| kQ |
(2)当液珠速度最大时k
| h2 |
得 h=
| 2 |
(3)设BC间的电势差大小UCB,由题意得
UCB=?C-?B=
| kQ |
| H |
| kQ |
| rB |
对由释放至液珠到达最高点(速度为零)的全过程应用动能定理得qUCB-mg(rB-H)=0
即q(
| kQ |
| H |
| kQ |
| rB |
将第(1)问的结果代入化简 rB2-3HrB+2H2=0
解得rB=2H rB′=H(舍去)
答:(1)液珠的比荷为
| q |
| m |
| 2gH2 |
| kQ |
(2)液珠速度最大时离A点的距离h=
| 2 |
(3)液珠能到达的最高点B离A点的高度为2H.
点评:解决本题的关键知道液珠的加速度为零时,速度最大,以及能够熟练运用动能定理和电场力做功公式W=qU.

练习册系列答案
相关题目
 如图所示,在A点固定一点电荷,电荷量为+Q,已知点电荷Q周围各点的电势φ=k
如图所示,在A点固定一点电荷,电荷量为+Q,已知点电荷Q周围各点的电势φ=k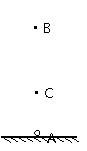

 ,其中r为该点到Q的距离(选无限远的电势为零)。求液珠能到达的最高点B离A点的高度
,其中r为该点到Q的距离(选无限远的电势为零)。求液珠能到达的最高点B离A点的高度 。
。
 ,其中r为该点到Q的距离(选无限远的电势为零)。求液珠能到达的最高点B离A点的高度rB。
,其中r为该点到Q的距离(选无限远的电势为零)。求液珠能到达的最高点B离A点的高度rB。