题目内容
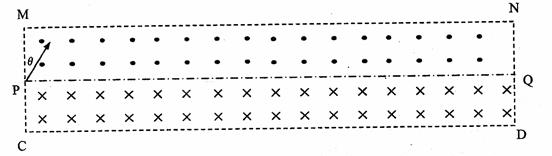
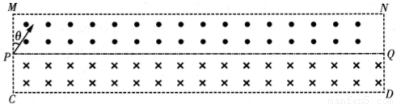
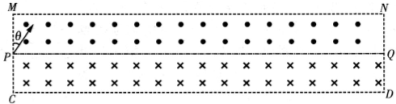
如图所示，中轴线PQ将矩形区域MNDC分成上下两部分，上部分充满垂直纸面向外的匀强磁场，下部分充满垂直纸面向内的匀强磁场，磁感应强度皆为B．一质量为m，带电量为q的带正电粒子从P点进入磁场，速度与边MC的夹角θ=30°．MC边长为a，MN边长为8a，不计粒子重力．求：（1）若要该粒子不从MN边射出磁场，其速度最大值是多少？
（2）若要该粒子恰从Q点射出磁场，其在磁场中的运行时间最少是多少？
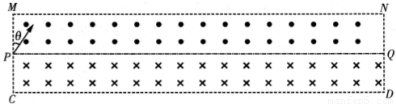
【答案】分析：（1）带电粒子进入磁场后，做匀速圆周运动，当该粒子恰好不从MN边射出磁场时，轨迹与MN相切，根据几何知识求出轨迹的半径，由牛顿第二定律求解速度的最大值．
（2）由几何知识得知，θ=30°，粒子每经过分界线PQ一次，在PQ方向前进的位移为轨迹半径的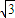
，粒子进入磁场后第n次经过PQ线时恰好到达Q点，则有n
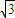r=8a，是正整数，而且r＜a，再根据周期公式求出最少时间．
解答：解：（1）设该粒子恰不从MN边射出磁场时的轨迹半径为r，由几何关系得：
rcos60°=r-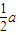
，解得 r=a
又由 qvB=m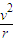
解得最大速度为 v=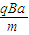
（2）粒子每经过分界线PQ一次，在PQ方向前进的位移为轨迹半径R的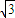
倍．
有 n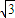
R=8a，且R＜a
解得 n＞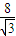
=4.62
n所能取的最小自然数为5．
粒子做圆周运动的周期为 T=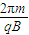
粒子每经过PQ分界线一次用去的时间为 t=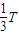
=
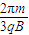
粒子到达Q点的最短时间为 tmin=5t=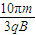
答：（1）若要该粒子不从MN边射出磁场，其速度最大值是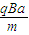
．
（2）若要该粒子恰从Q点射出磁场，其在磁场中的运行时间最少是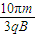
．
点评：本题中带电粒子的运动具有周期性，要运用数学上分析数列通项的方法进行研究，同时要考虑临界条件．
（2）由几何知识得知，θ=30°，粒子每经过分界线PQ一次，在PQ方向前进的位移为轨迹半径的
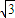，粒子进入磁场后第n次经过PQ线时恰好到达Q点，则有n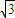r=8a，是正整数，而且r＜a，再根据周期公式求出最少时间．解答：解：（1）设该粒子恰不从MN边射出磁场时的轨迹半径为r，由几何关系得：
rcos60°=r-
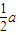，解得 r=a 又由 qvB=m
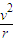
解得最大速度为 v=
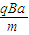
（2）粒子每经过分界线PQ一次，在PQ方向前进的位移为轨迹半径R的
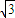倍．有 n
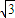R=8a，且R＜a 解得 n＞
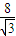=4.62n所能取的最小自然数为5．
粒子做圆周运动的周期为 T=
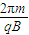
粒子每经过PQ分界线一次用去的时间为 t=
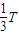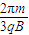
= 粒子到达Q点的最短时间为 tmin=5t=
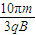
答：（1）若要该粒子不从MN边射出磁场，其速度最大值是
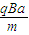．（2）若要该粒子恰从Q点射出磁场，其在磁场中的运行时间最少是
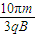．点评：本题中带电粒子的运动具有周期性，要运用数学上分析数列通项的方法进行研究，同时要考虑临界条件．
练习册系列答案
智慧小复习系列答案
相关题目
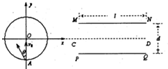如图所示，在竖直平面直角坐标xOy内有半径为R、圆心在O点、与xOy平面垂直的圆形匀强磁场，右侧有水平放置的两块带电金属板MN、PQ平行正对，极板长度为l1，板间距为d板间存在着方向竖直的匀强电场．一质量为m且电荷量为q的粒子（不计重力及空气阻力）以速度v0从A处沿y轴正向进入圆形匀强磁场，并沿x轴正向离开圆形匀强磁场，然后从两极板的左端沿中轴线CD射入匀强电场，恰好打在上板边沿N端．
。MC边长为a，MN边长为8a，不计粒子重力。求：
