题目内容
如图所示,水平面内有两根互相平行且足够长的光滑金属轨道,它们间的距离L="0.20" m,在两轨道的左端之间接有一个R=0.10 的电阻。在虚线OO′(OO′垂直于轨道)右侧有方向竖直向下的匀强磁场,磁感应强度B=0.50T。一根质量m=0.10kg的直金属杆
的电阻。在虚线OO′(OO′垂直于轨道)右侧有方向竖直向下的匀强磁场,磁感应强度B=0.50T。一根质量m=0.10kg的直金属杆 垂直于轨道放在两根轨道上。某时刻杆
垂直于轨道放在两根轨道上。某时刻杆 以
以 =2.0m/s且平行于轨道的初速度进入磁场,同时在杆上施加一个水平拉力,使其以
=2.0m/s且平行于轨道的初速度进入磁场,同时在杆上施加一个水平拉力,使其以 =2.0m/s2的加速度做匀减速直线运动。杆
=2.0m/s2的加速度做匀减速直线运动。杆 始终与轨道垂直且它们之间保持良好接触。杆
始终与轨道垂直且它们之间保持良好接触。杆 和轨道的电阻均可忽略。
和轨道的电阻均可忽略。
(1)请你通过计算判断,在金属杆 向右运动的过程中,杆上所施加的水平拉力的方向;
向右运动的过程中,杆上所施加的水平拉力的方向;
(2)在金属杆 向右运动的过程中,求杆中的感应电流为最大值的
向右运动的过程中,求杆中的感应电流为最大值的 时,水平拉力的大小;
时,水平拉力的大小;
(3)从金属杆 进入磁场至速度减为零的过程中,电阻R上发出的热量Q=0.13J,求此过程中水平拉力做的功。
进入磁场至速度减为零的过程中,电阻R上发出的热量Q=0.13J,求此过程中水平拉力做的功。
(1)杆上所施加的水平拉力的方向始终向左 (2)0.15N(3)-7.0×10-2J
解析试题分析:(1)金属杆刚进入磁场时,杆中的感应电流

此时,杆 所受的安培力
所受的安培力 ,方向水平向左
,方向水平向左
杆 所受的合力
所受的合力 ,方向水平向左
,方向水平向左
在金属杆 向右做匀减速直线运动的过程中,安培力
向右做匀减速直线运动的过程中,安培力 不断减小
不断减小
因此,杆上所施加的水平拉力的方向始终向左。
(2)当速度减为 时,电流为
时,电流为
此时杆 所受的安培力
所受的安培力 ,方向水平向左
,方向水平向左
根据牛顿第二定律
水平拉力的大小
(3)由动能定理
其中克服安培力做功的数值等于电阻R上发出的热量Q,即
所以 J
J
考点:此题为电磁感应与动力学问题的综合题目。考查法拉第电磁感应定律、楞次定律、牛顿第二定律及能量守恒定律。

质量为m的汽车,发动机功率恒为P,摩擦力f,牵引力F,汽车静止开始,经时间t行驶位移L时,速度达最大Vm,求发动机所做的功( )
| A.Pt | B.fvmt | C. +fL +fL | D.FL |
汽车在平直公路上以恒定的功率启动,它受到的阻力大小不变,则下列说法正确的是 ( )
| A.牵引力F大小不变,加速度a也大小不变 |
| B.F逐渐增大,a也逐渐增大 |
| C.当牵引力等于阻力时,汽车速度达到最大 |
| D.启动过程中汽车的速度均匀增加 |
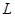 、半径为
、半径为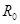 的内壁光滑的
的内壁光滑的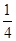 圆弧固定轨道,右端通过导线接有阻值为
圆弧固定轨道,右端通过导线接有阻值为 的电阻,圆弧轨道处于竖直向上的匀强磁场中,磁场的磁感应强度为
的电阻,圆弧轨道处于竖直向上的匀强磁场中,磁场的磁感应强度为 。质量为
。质量为 、电阻为
、电阻为 、长度也为
、长度也为 处由静止开始下滑,到达底端
处由静止开始下滑,到达底端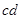 时,对轨道的压力恰好等于金属棒的重力2倍,不计导轨和导线的电阻,空气阻力忽略不计,重力加速度为
时,对轨道的压力恰好等于金属棒的重力2倍,不计导轨和导线的电阻,空气阻力忽略不计,重力加速度为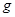 。求:
。求: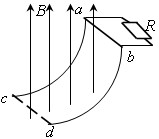
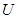 多大;
多大;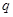 ;
;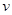 从轨道的低端
从轨道的低端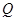 。
。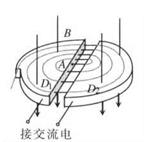
 圆弧轨道,半径为r、间距为L,轨道电阻不计.在轨道顶端连有一阻值为R的电阻,整个装置处在一竖直向上的匀强磁场中,磁感应强度为B.现有一根长度稍大于L、质量为m、电阻不计的金属棒从轨道的顶端ab处由静止开始下滑,到达轨道底端cd时受到轨道的支持力为2mg.整个过程中金属棒与导轨电接触良好,求:
圆弧轨道,半径为r、间距为L,轨道电阻不计.在轨道顶端连有一阻值为R的电阻,整个装置处在一竖直向上的匀强磁场中,磁感应强度为B.现有一根长度稍大于L、质量为m、电阻不计的金属棒从轨道的顶端ab处由静止开始下滑,到达轨道底端cd时受到轨道的支持力为2mg.整个过程中金属棒与导轨电接触良好,求:
 (k未知且k>0),E、F为磁场边界,且与C、D板平行。D板右方分布磁场大小均为B0,方向如图所示的匀强磁场。区域Ⅰ的磁场宽度为d,区域Ⅱ的磁场宽度足够大。在C板小孔附近有质量为m、电量为q的负离子由静止开始加速后,经D板小孔垂直进入磁场区域Ⅰ,不计离子重力。
(k未知且k>0),E、F为磁场边界,且与C、D板平行。D板右方分布磁场大小均为B0,方向如图所示的匀强磁场。区域Ⅰ的磁场宽度为d,区域Ⅱ的磁场宽度足够大。在C板小孔附近有质量为m、电量为q的负离子由静止开始加速后,经D板小孔垂直进入磁场区域Ⅰ,不计离子重力。
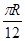 。现有电荷量为e、质量为m的电子在O点正下方负极板上的P点由静止释放。不计电子所受重力。
。现有电荷量为e、质量为m的电子在O点正下方负极板上的P点由静止释放。不计电子所受重力。
