题目内容
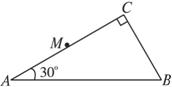
(8分)一棱镜的截面为直角三角形ABC,∠A=30°,斜边AB=a。棱镜材料的折射率为n=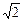 。在此截面所在的平面内,一条光线以45°的入射角从AC边的中点M射入棱镜射出的点的位置(不考虑光线沿原来路返回的情况)。
。在此截面所在的平面内,一条光线以45°的入射角从AC边的中点M射入棱镜射出的点的位置(不考虑光线沿原来路返回的情况)。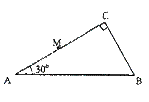
解:设入射角为i,折射角为r,由折射定律得 :
: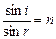 ①
① 由已知条件及①式得
由已知条件及①式得 :r=30° ②(2分)
:r=30° ②(2分)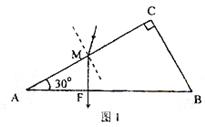
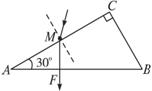
 如果入射光线在法线的右侧,光路图如图1所示。设出射点为F,由几何关系可得:
如果入射光线在法线的右侧,光路图如图1所示。设出射点为F,由几何关系可得: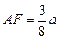
 ③
③ 即出射点在AB边上离A点
即出射点在AB边上离A点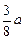 的位置。(2分)
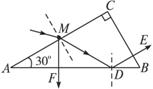
的位置。(2分) 如果入射光线在法线的左侧,光路图如图2所示。设折射光线与AB的交点为D。
如果入射光线在法线的左侧,光路图如图2所示。设折射光线与AB的交点为D。 由几何关系可知,在D点的入射角:q=60°
由几何关系可知,在D点的入射角:q=60° ④
④ 设全发射的临界角为qC,则
设全发射的临界角为qC,则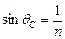
 ⑤
⑤  由⑤和已知条件得:qC=45°
由⑤和已知条件得:qC=45° ⑥
⑥ 因此,光在D点全反射。(2分)
因此,光在D点全反射。(2分)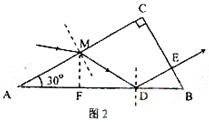
 设此光线的出射点为E,由几何关系得:
设此光线的出射点为E,由几何关系得: ∠DEB=90°
∠DEB=90° BD=a-2AF ⑦
BD=a-2AF ⑦
BE= Bdsin30° ⑧
Bdsin30° ⑧ 联立③⑦⑧式得:
联立③⑦⑧式得: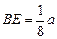
 ⑨
⑨ 即出射点在BC边上离B点
即出射点在BC边上离B点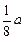 的位置。(2分)
的位置。(2分)
解析

练习册系列答案
相关题目
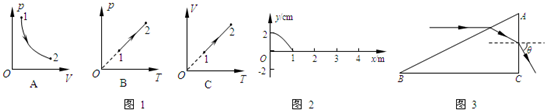
 (2011?攀枝花三模)用如图所示的装置可以测定棱镜的折射率,其中ABC表示待测直角棱镜的横截面,棱镜的两个锐角α和β都是已知的,紧贴直角边AC的是一块平面镜,将一束光线SO入射到棱镜的AB面上,适当调整SO的入射方向,使从AB面出射的光线与入射光线SO恰好重合,在这种情况下,仅需要测出SO与AB间的夹角γ就可以算出该棱镜的折射率,则计算折射率的表达式为( )
(2011?攀枝花三模)用如图所示的装置可以测定棱镜的折射率,其中ABC表示待测直角棱镜的横截面,棱镜的两个锐角α和β都是已知的,紧贴直角边AC的是一块平面镜,将一束光线SO入射到棱镜的AB面上,适当调整SO的入射方向,使从AB面出射的光线与入射光线SO恰好重合,在这种情况下,仅需要测出SO与AB间的夹角γ就可以算出该棱镜的折射率,则计算折射率的表达式为( ) 如图所示,△ABC为一直角三棱镜的截面,其顶角θ=30°,P为垂直于直线BCD的光屏.一束宽度等于AB的单色平行光束垂直射向AB面,经三棱镜折射后在屏P上形成一条光带.
如图所示,△ABC为一直角三棱镜的截面,其顶角θ=30°,P为垂直于直线BCD的光屏.一束宽度等于AB的单色平行光束垂直射向AB面,经三棱镜折射后在屏P上形成一条光带. (选做题)(请从A、B和C三小题中选定两小题作答,并在答题卡相应的答题区域内作答,如都作答则按A、B两小题评分)
(选做题)(请从A、B和C三小题中选定两小题作答,并在答题卡相应的答题区域内作答,如都作答则按A、B两小题评分)