题目内容
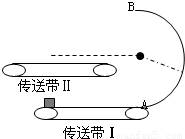
质量为m=2kg的工件轻放到以速度v1=10m/s水平向右匀速传动的传送带Ⅰ的最左端,(传送带Ⅰ绷紧且足够长),经与其上表面相切的竖直放置的光滑半圆形轨道传送到向左运动的传送带Ⅱ上,如图所示.已知光滑半圆形轨道半径为1.6m,传送带Ⅱ的上表面比半圆形轨道的圆心低0.2m.重力加速度g=10m/s2.(1)若工件与传送带Ⅰ的滑动摩擦因素μ=0.5,试求工件相对传送带Ⅰ滑行的距离为多少?
(2)工件到达半圆形轨道的最低端A点时对轨道的压力为多少?
(3)传送带Ⅱ的右端(传动轮大小不计)距离半圆形轨道的圆心的水平距离最短为多少?
【答案】分析:(1)根据牛顿第二定律求加速度,根据运动学公式求相对滑动的时间和对应的传送带位移和滑块位移,最后得出相对位移;
(2)工件受到的重力和支持力的合力等于向心力,根据牛顿第二定律列式求解;
(3)先根据机械能守恒定律求出滑块到达最高点的速度,然后根据平抛运动的位移公式求滑块的落点,从而确定传送带最右端与圆心的最小距离.
解答:解:(1)由f=μmg可得a=5m/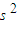 ;
;
对于工件 t=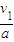 =2s
=2s
对传送带Ⅰ有S1=v1t=20m,对于工件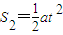 =10m
=10m
△S=S1-S2=10m
即工件相对传送带Ⅰ滑行的距离为10m.
(2)工件是以速度v1到达A点
根据FN-mg=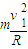
解得
FN=mg+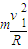 =145N
=145N
即工件到达半圆形轨道的最低端A点时对轨道的压力为145N.
(3)设A点重力势能为零,工件到达B点时的速度为v2,根据机械能守恒定律可得
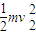 +2mgR=
+2mgR=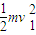
解得
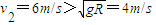
根据平抛运动可得
x=v2t′
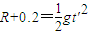
解得
x=3.6m
即传送带Ⅱ的右端(传动轮大小不计)距离半圆形轨道的圆心的水平距离最短为为3.6m.
点评:本题关键是根据机械能守恒定律求出各个特殊位置的速度,然后根据向心力公式求压力,根据平抛运动的位移公式求落点.
(2)工件受到的重力和支持力的合力等于向心力,根据牛顿第二定律列式求解;
(3)先根据机械能守恒定律求出滑块到达最高点的速度,然后根据平抛运动的位移公式求滑块的落点,从而确定传送带最右端与圆心的最小距离.
解答:解:(1)由f=μmg可得a=5m/
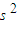 ;
;对于工件 t=
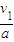 =2s
=2s对传送带Ⅰ有S1=v1t=20m,对于工件
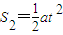 =10m
=10m△S=S1-S2=10m
即工件相对传送带Ⅰ滑行的距离为10m.
(2)工件是以速度v1到达A点
根据FN-mg=
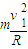
解得
FN=mg+
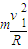 =145N
=145N即工件到达半圆形轨道的最低端A点时对轨道的压力为145N.
(3)设A点重力势能为零,工件到达B点时的速度为v2,根据机械能守恒定律可得
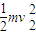 +2mgR=
+2mgR=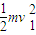
解得
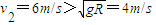
根据平抛运动可得
x=v2t′
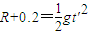
解得
x=3.6m
即传送带Ⅱ的右端(传动轮大小不计)距离半圆形轨道的圆心的水平距离最短为为3.6m.
点评:本题关键是根据机械能守恒定律求出各个特殊位置的速度,然后根据向心力公式求压力,根据平抛运动的位移公式求落点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2005?南通一模)如图所示在水平面上有两条相互平行的光滑绝缘导轨,两导轨间距工L=1m,导轨的虚线范围内有一垂直导轨平面的匀强磁场,磁感应强度B=0.2T,磁场宽度S大于L,左、右两边界与导轨垂直.有一质量m=0.2kg,电阻 r=0.1Ω边长也为L正方形金属框以某一初速度,沿导轨向右进入匀强磁场.最终金属框只能有-半面积离开磁场区域
(2005?南通一模)如图所示在水平面上有两条相互平行的光滑绝缘导轨,两导轨间距工L=1m,导轨的虚线范围内有一垂直导轨平面的匀强磁场,磁感应强度B=0.2T,磁场宽度S大于L,左、右两边界与导轨垂直.有一质量m=0.2kg,电阻 r=0.1Ω边长也为L正方形金属框以某一初速度,沿导轨向右进入匀强磁场.最终金属框只能有-半面积离开磁场区域