题目内容
A、B两球质量分别为m1与m2，用一劲度系数为k的弹簧相连，一长为l1的细线与m1相连，置于水平光滑桌面上，细线的另一端拴在竖直轴OO′ 上，如图所示。当m1与m2均以角速度ω绕OO′ 做匀速圆周运动时，弹簧长度为l2，求：
（1）此时弹簧伸长量；
（2）绳子张力；
（3）将线突然烧断瞬间A球的加速度大小。
【答案】
解：（1）弹簧弹力提供B球做匀速圆周运动的向心力，弹簧伸长量X
KX=m2(l1+l2)
2
（5分）
则 X=
，
（2分）
(2) A球做匀速圆周运动，绳拉力F
F－KX=m1l12
（5分）
则 F= 
（2分）
(3)绳烧断瞬间，A受弹簧弹力为 KX，
A球的加速度大小 则 KX=m1a （5分）
所以 a= 
（1分）
练习册系列答案
相关题目
A、B两球质量分别为m1与m2，用一劲度系数为K的弹簧相连，一长为l1的细线与m1相连，置于水平光滑桌面上，细线的另一端拴在竖直轴OO′上，如图所示，当m1与m2均以角速度ω绕OO′做匀速圆周运动时，弹簧长度为l2．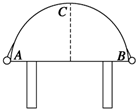
如图所示，A、B两球质量分别为4m和5m，其间用轻绳连接，跨放在光滑的半圆柱体上（半圆柱体的半径为R）．两球从水平直径的两端由静止释放．已知重力加速度为g，圆周率用π表示．当球A到达最高点C时，求：
A、B两球质量分别为m1和m2，用一劲度系数为k的弹簧相连，一长为l1的细线与m1相连，置于水平光滑桌面上，细线的另一端拴在数值轴OO′上，如图所示．当m1与m2均以角速度ω绕OO′做匀速圆周运动且稳定后，弹簧长度为l2．求：
A、B两球之间压缩一根轻弹簧，静置于光滑水平桌面上．已知A、B两球质量分别为2m和m．当用板挡住A球而只释放B球时，B球被弹出落于距桌面水平距离为s的水平地面上，如图，问当用同样的程度压缩弹簧，取走A左边的挡板，将A、B同时释放，B球的落地点距桌面距离为（ ）
在光滑的绝缘水平面上，A、B两球（可以看成质点）位于x轴上，A球带电，B球不带电，开始时B球静置于场强为E＝1×103 N/C的水平匀强电场的边缘（如图1所示），A球从
原点开始经过2s后恰好与B碰撞，碰后合为一体在电场中运动，A、B系统的动能与坐标的部分关系如图2所示，则：