��Ŀ����
��ͼ��ʾ����Ϊ2L����ˣ����˸��̶�һС��A������Ϊm1��B������Ϊm2����m1��m2�����˵��е�O��һˮƽ�⻬�̶��ᣬ�˿��ڲ�ͬ�ij�ʼ��������������ֱƽ����ת��������˵������ȷ���ǣ�������

| A��A����ߵ���ٶȿ���Ϊ�� | ||||
| B��B����͵���ٶ�һ����Ϊ�� | ||||
C�����˶����������Ϊ�㣬���ʱ�˵Ľ��ٶ�Ϊ
| ||||
| D��ͼʾλ�ø˶�B�����С����һ����Ϊm2g |

A����ģ��A����ߵ���ٶȿ���Ϊ�㣮��A���ٶ�Ϊ��ʱ��B���ٶ�ҲΪ�㣮��A��ȷ��B����
C������͵��У�F2-m2g=m2L��2�����F2=m2g+m2L��2������ߵ㣬�У�F1+m1g=mL��2�����F1=mL��2-m1g����F1=F2����æ�=
����C��ȷ��
D����ͼʾλ�ã�B�����С�ٶ�Ϊ�㣬����С����Ϊm2g����D����
��ѡAC��
C������͵��У�F2-m2g=m2L��2�����F2=m2g+m2L��2������ߵ㣬�У�F1+m1g=mL��2�����F1=mL��2-m1g����F1=F2����æ�=
|
D����ͼʾλ�ã�B�����С�ٶ�Ϊ�㣬����С����Ϊm2g����D����
��ѡAC��

��ϰ��ϵ�д�
 ���ݼ���ϵ�д�
���ݼ���ϵ�д�
�����Ŀ
 ��ͼ��ʾ����Ϊ2L����ˣ����˸��̶�һС��A������Ϊm1��B������Ϊm2�����˵��е�O��һˮƽ�⻬�̶��ᣬ�˿���������ֱƽ����ת������ת������ֱλ����A�����϶ˣ�B�����¶�ʱ�˵Ľ��ٶ�Ϊ�أ���ʱ�˶�ת���������Ϊ�㣬��A��B��С�������֮��Ϊ��������
��ͼ��ʾ����Ϊ2L����ˣ����˸��̶�һС��A������Ϊm1��B������Ϊm2�����˵��е�O��һˮƽ�⻬�̶��ᣬ�˿���������ֱƽ����ת������ת������ֱλ����A�����϶ˣ�B�����¶�ʱ�˵Ľ��ٶ�Ϊ�أ���ʱ�˶�ת���������Ϊ�㣬��A��B��С�������֮��Ϊ��������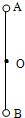 ��ͼ��ʾ����Ϊ2L����ˣ����˸��̶�һС��A������Ϊm1��B������Ϊm2����m1��m2�����˵��е�O��һˮƽ�⻬�̶��ᣬ�˿��ڲ�ͬ�ij�ʼ��������������ֱƽ����ת��������˵������ȷ���ǣ�������
��ͼ��ʾ����Ϊ2L����ˣ����˸��̶�һС��A������Ϊm1��B������Ϊm2����m1��m2�����˵��е�O��һˮƽ�⻬�̶��ᣬ�˿��ڲ�ͬ�ij�ʼ��������������ֱƽ����ת��������˵������ȷ���ǣ�������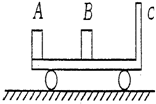 ��ͼ��ʾ����Ϊ2L�İ���⻬�Ҳ������ƽ��С��C���ڹ⻬ˮƽ���ϣ������Ҷ��е��壬��������mC=4m�����ھ�ֹ��ƽ�峵����˷�һ��������Ϊ+q������Ϊm�����A�����м�λ�÷�һ����Ե����B������ΪmB=2m���������ռ����һ��ˮƽ�������ǿ�糡ʱ��������A�ɾ�ֹ��ʼ�����˶��������ٶ�v0��B������ײ������A��
��ͼ��ʾ����Ϊ2L�İ���⻬�Ҳ������ƽ��С��C���ڹ⻬ˮƽ���ϣ������Ҷ��е��壬��������mC=4m�����ھ�ֹ��ƽ�峵����˷�һ��������Ϊ+q������Ϊm�����A�����м�λ�÷�һ����Ե����B������ΪmB=2m���������ռ����һ��ˮƽ�������ǿ�糡ʱ��������A�ɾ�ֹ��ʼ�����˶��������ٶ�v0��B������ײ������A�� ��2005?����һģ����ͼ��ʾ����Ϊ2L�İ���⻬�Ҳ������ƽ��С��C���ڹ⻬ˮƽ���ϣ������Ҷ��е��壬��������mC=4m�����ھ�ֹ��ƽ�峵����˷�һ���������Ϊ+q������ΪmA=m�Ľ�����A������һ��ԵС���B����ƽ�峵�����룬���B������mB=2m���������ռ����һ��ˮƽ�������ǿ�糡ʱ��������A�ɾ�ֹ��ʼ�����˶���A���ٶ�v0��B������ײ������A��v0/4���ٶȷ���������B��һ���ٶ���ƽ�������˶���C���ĵ�������������С�����ٶȵ�����ǰ���B�ٶȵ�һ�룮���A��B����Ϊ�ʵ㣬A��B����ʱ���������Զ���ڵ糡������
��2005?����һģ����ͼ��ʾ����Ϊ2L�İ���⻬�Ҳ������ƽ��С��C���ڹ⻬ˮƽ���ϣ������Ҷ��е��壬��������mC=4m�����ھ�ֹ��ƽ�峵����˷�һ���������Ϊ+q������ΪmA=m�Ľ�����A������һ��ԵС���B����ƽ�峵�����룬���B������mB=2m���������ռ����һ��ˮƽ�������ǿ�糡ʱ��������A�ɾ�ֹ��ʼ�����˶���A���ٶ�v0��B������ײ������A��v0/4���ٶȷ���������B��һ���ٶ���ƽ�������˶���C���ĵ�������������С�����ٶȵ�����ǰ���B�ٶȵ�һ�룮���A��B����Ϊ�ʵ㣬A��B����ʱ���������Զ���ڵ糡������