题目内容
3. 如图所示,竖直环A半径为r,固定在木板B上,木板B放在水平地面上,B的左右两侧各有一固定在地上的挡板,使B不能左右运动,在环的最低点静置一小球C,A、B、C的质量均为m.给小球一水平向右的瞬时速度,小球会在环内侧做圆周运动,为保证小球能通过环的最高点,且不会使环在竖直方向上跳起,则小球在最高点的速度必须满足什么条件?
如图所示,竖直环A半径为r,固定在木板B上,木板B放在水平地面上,B的左右两侧各有一固定在地上的挡板,使B不能左右运动,在环的最低点静置一小球C,A、B、C的质量均为m.给小球一水平向右的瞬时速度,小球会在环内侧做圆周运动,为保证小球能通过环的最高点,且不会使环在竖直方向上跳起,则小球在最高点的速度必须满足什么条件?
分析 小球能通过最高点的临界情况是轨道对小球的弹力为零,靠重力提供向心力,根据牛顿第二定律求出最高点的最小速度.为了不会使环在竖直方向上跳起,在最高点,环对小球的作用力不能超过A和B的重力,结合牛顿第二定律求出最高点的最大速度.
解答 解:在最高点,速度最小时有:$mg=m\frac{{{v}_{1}}^{2}}{r}$,解得:${v}_{1}=\sqrt{gr}$,
在最高点,速度最大时有:$mg+F=m\frac{{{v}_{2}}^{2}}{r}$,F=2mg,解得:${v}_{2}=\sqrt{3gr}$,
所以保证小球能通过环的最高点,且不会使环在竖直方向上跳起,在最高点的速度范围为$\sqrt{gr}≤v≤\sqrt{3gr}$.
答:小球在最高点的速度必须满足$\sqrt{gr}≤v≤\sqrt{3gr}$.
点评 本题考查了牛顿第二定律和圆周运动的运用,关键理清在最高点的两个临界情况,求出在最高点的最大速度和最小速度.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
18.A、B两物体各自做直线运动的图线分别如图甲、乙所示,则( )


| A. | 离出发点最远的在甲图中是b,在乙图中是c | |
| B. | 离出发点最远的在甲图中是c,在乙图中是b | |
| C. | 离出发点最近的在甲图中是c,在乙图中是c | |
| D. | 离出发点最近的在甲图中是a,在乙图中是a |
18.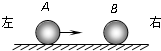 如图所示,光滑水平面上有两个大小相同的钢球A、B,A球的质量大于B球的质量.开始时A球以一定的速度向右运动,B球处于静止状态.两球碰撞后A球向左运动,B球向右运动.设碰撞前A球的德布罗意波长为λ1,碰撞后A、B两球的德布罗意波长分别为λ2和λ3,则下列关系正确的是( )
如图所示,光滑水平面上有两个大小相同的钢球A、B,A球的质量大于B球的质量.开始时A球以一定的速度向右运动,B球处于静止状态.两球碰撞后A球向左运动,B球向右运动.设碰撞前A球的德布罗意波长为λ1,碰撞后A、B两球的德布罗意波长分别为λ2和λ3,则下列关系正确的是( )
 如图所示,光滑水平面上有两个大小相同的钢球A、B,A球的质量大于B球的质量.开始时A球以一定的速度向右运动,B球处于静止状态.两球碰撞后A球向左运动,B球向右运动.设碰撞前A球的德布罗意波长为λ1,碰撞后A、B两球的德布罗意波长分别为λ2和λ3,则下列关系正确的是( )
如图所示,光滑水平面上有两个大小相同的钢球A、B,A球的质量大于B球的质量.开始时A球以一定的速度向右运动,B球处于静止状态.两球碰撞后A球向左运动,B球向右运动.设碰撞前A球的德布罗意波长为λ1,碰撞后A、B两球的德布罗意波长分别为λ2和λ3,则下列关系正确的是( )| A. | λ1=$\frac{{λ}_{2}{λ}_{3}}{{λ}_{2}-{λ}_{3}}$ | B. | λ1=$\frac{{λ}_{2}{λ}_{3}}{{λ}_{2}+{λ}_{3}}$ | ||
| C. | λ1=2λ2=3λ3 | D. | λ1=λ2-λ3 |
8. 一简谐横波以2m/s的波速沿x轴正方向传播,已知t=0时的波形如图所示,则( )
一简谐横波以2m/s的波速沿x轴正方向传播,已知t=0时的波形如图所示,则( )
 一简谐横波以2m/s的波速沿x轴正方向传播,已知t=0时的波形如图所示,则( )
一简谐横波以2m/s的波速沿x轴正方向传播,已知t=0时的波形如图所示,则( )| A. | 波的波长λ=4m | |
| B. | x=0处的质点在t=0时向y轴正方向运动 | |
| C. | x=0处的质点在t=$\frac{1}{12}$s时速度值最大 | |
| D. | x=0处的质点在t=$\frac{1}{6}$s时速度值最大 | |
| E. | x=0处的质点在2 s内路程0.16 m |
13.公路上的雷达测速仪的工作原理是利用( )
| A. | 波的反射和多普勒效应 | B. | 波的干涉和多普勒效应 | ||
| C. | 波的干涉和波的反射 | D. | 波的共振 |
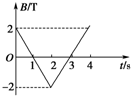 一个面积S=4×10-2m2,匝数n=100匝的线圈,放在匀强磁场中,磁场方向垂直平面,磁感应强度的大小随时间变化规律如图所示,在开始2秒内穿过线圈的磁通量的变化率等于8×10-2Wb/s,在第3秒末感应电动势大小为8V.
一个面积S=4×10-2m2,匝数n=100匝的线圈,放在匀强磁场中,磁场方向垂直平面,磁感应强度的大小随时间变化规律如图所示,在开始2秒内穿过线圈的磁通量的变化率等于8×10-2Wb/s,在第3秒末感应电动势大小为8V.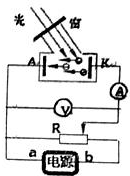 利用如图装置和已知频率γ1,γ2的两种光可以测出普朗克常量h.则所加的电源正极为b (填a或b):实验的主要步骤及还需测量的物理量为:
利用如图装置和已知频率γ1,γ2的两种光可以测出普朗克常量h.则所加的电源正极为b (填a或b):实验的主要步骤及还需测量的物理量为: