题目内容
一个半球形的碗放在桌面上，碗口水平，O点为其球心，碗的内表面及碗口是光滑的．一根细线跨在碗口上，线的两端分别系有质量为m1和 m2的小球，当它们处于平衡状态时，质量为m1的小球与O点的连线与水平线的夹角为α=60°．求两小球的质量之比| m1 | m2 |
分析：两物体均处于静止状态，可分别对两物体进行受力分析应用平衡条件列式求解．
解答：解：对质量为m2的物体受力分析：受重力和拉力，由平衡条件得：绳上的拉力大小T=m2g
对质量为m1的物体受力分析并合成如图：由平衡条件得：F′=m1g
因为角α是60°，所以三角形为等边三角形，画出来的平行四边形为菱形．
连接菱形对角线，对角线相互垂直，红色三角形为直角三角形：
由三角函数关系：
sinα=
=
=
由α=60°得：
=
即：
=
故答案为：
．
对质量为m1的物体受力分析并合成如图：由平衡条件得：F′=m1g
因为角α是60°，所以三角形为等边三角形，画出来的平行四边形为菱形．
连接菱形对角线，对角线相互垂直，红色三角形为直角三角形：
由三角函数关系：
sinα=
| ||
| T |
| ||
| T |
| m1g |
| 2m2g |
由α=60°得：
| m1g |
| 2m2g |
| ||
| 2 |
即：
| m1 |
| m2 |
| 3 |
故答案为：
| 3 |
点评：本题关键是先对两物体受力分析，然后根据共点力平衡条件列式求解，求解过程中注意寻找直角三角形．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
如图所示，一个半球形的碗放在桌面上，碗口水平，O点为其球心，碗的内表面及碗口是光滑的，一根细线跨在碗口上，线的两端分别系有质量为m1和m2的小球，当它们处于平衡状态时，质量为m1的小球与O点的连线与水平线的夹角为α=60°，两小球的质量比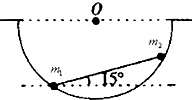
如图所示，一个半球形的碗放在桌面上，碗口水平，O点为其球心，碗的内表面是光滑的．一根质量可忽略的刚性细杆两端分别固定着质量为m1和m2的小球，放置在半球面内．已知细杆长度是球面半径的
如图所示，一个半球形的碗放在桌面上，碗口水平，O是球心，碗的内表面光滑．一根轻质杆的两端固定有两个小球，质量分别是m1，m2．当它们静止时，m1、m2与球心的连线跟水平面分别成60°，30°角，则碗对两小球的弹力大小之比是
如图所示，一个半球形的碗放在桌面上，碗口水平，O点为其球心，碗的内表面及碗口是光滑的．一根细线跨在碗口上，线的两端分别系有质量为m1和m2的小球，当它们处于平衡状态时，质量为m1的小球与O点的连线与水平线的夹角为α=60°．两小球的质量比m1/m2为（ ）